số tiếp tuyến đi qua điểm a(1;-6) của đồ thị hàm số y=x^3-3x+1

Những câu hỏi liên quan
Có hai tiếp tuyến của đồ thị hàm số
y
3
x
-
2
x
-
1
đi qua điểm A(9;0) Tích hệ số góc của hai tiếp tuyến đó bằng A.
-
3
8
B.
3
8
C.
9
64
D.
-
9
64
Đọc tiếp
Có hai tiếp tuyến của đồ thị hàm số y = 3 x - 2 x - 1 đi qua điểm A(9;0) Tích hệ số góc của hai tiếp tuyến đó bằng
A. - 3 8
B. 3 8
C. 9 64
D. - 9 64
Số tiếp tuyến đi qua điểm A(1;-6) của đồ thị hàm số y = x 3 - 3 x + 1 là:
A.0
B.2
C.1
D.3
Số tiếp tuyến đi qua điểm A(1;-6) của đồ thị hàm số y = x 3 - 3 x + 1 là:
A. 0
B. 2
C. 1
D. 3
Chọn C
Phương pháp:
Cho hàm số y = f(x) và M( x 0 ; y 0 )
Bước 1: Gọi ( ∆ ) là tiếp tuyến của đồ thị hàm số đã cho của đồ thị hàm số y = f(x); ( ∆ ) đi qua M( x 0 ; y 0 ) và có hệ số góc k.
Bước 2: (
∆
) có dạng 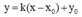
Để (
∆
) tiếp xúc với đồ thị y = f(x) thì hệ 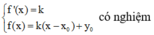
Bước 3: Giải hệ bằng phương pháp thế, số nghiệm của hệ là số tiếp tuyến ( ∆ ) tìm được.
Cách giải:
Gọi k là hệ số góc tiếp tuyến ( ∆ ) với đồ thị (C) đi qua A(1;-6)
=>( ∆ ) có dạng: y = k(x-1) - 6
Để (
∆
) tiếp xúc với (C) thì 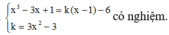
![]()
![]()
![]()
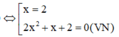
Vậy có 1 pttt đi qua A(1;-6).
Đúng 0
Bình luận (0)
Tìm số tiếp tuyến của đồ thị hàm số
y
4
x
3
-
6
x
2
+
1
, biết tiếp tuyến đó đi qua điểm
M
(
-
1
;
-
9
)
A. 3 B. 2 C. 0 D. 1
Đọc tiếp
Tìm số tiếp tuyến của đồ thị hàm số y = 4 x 3 - 6 x 2 + 1 , biết tiếp tuyến đó đi qua điểm M ( - 1 ; - 9 )
A. 3
B. 2
C. 0
D. 1
Cho hàm số \(y=\dfrac{2x+2}{x-1}\) (C). Viết pt tiếp tuyến của đồ thị (C) biết
a) tung độ tiếp điểm bằng -2
b) tiếp tuyến song song với đg thg d: \(y=-4x+1\)
c) tiếp tuyến đi qua điểm \(A\left(4;3\right)\)
d) tiếp tuyến tạo với 2 trục tọa độ 1 tam giác vuông cân
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
a. \(\dfrac{2x+2}{x-1}=-2\Rightarrow2x+2=-2x+2\Rightarrow x=0\Rightarrow y'\left(0\right)=-4\)
Phương trình tiếp tuyến: \(y=-4\left(x-0\right)-2\)
b. Tiếp tuyến song song đường thẳng đã cho nên có hệ số góc k=-4
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-2\\x=2\Rightarrow y=6\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4\left(x-0\right)-2\\y=-4\left(x-2\right)+6\end{matrix}\right.\)
c. Gọi \(M\left(x_0;y_0\right)\) là tọa độ tiếp điểm
Pt tiếp tuyến qua M có dạng: \(y=\dfrac{-4}{\left(x_0-1\right)^2}\left(x-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)
Do tiếp tuyến qua A nên:
\(3=\dfrac{-4}{\left(x_0-1\right)^2}\left(4-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)
\(\Leftrightarrow x_0^2-10x_0+21=0\Rightarrow\left[{}\begin{matrix}x_0=3\Rightarrow y'\left(3\right)=-1;y\left(3\right)=4\\x_0=7;y'\left(7\right)=-\dfrac{1}{9};y\left(7\right)=\dfrac{8}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-\dfrac{1}{9}\left(x-7\right)+\dfrac{8}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
d.
Do tiếp tuyến tạo với 2 trục tọa độ 1 tam giác vuông cân nên có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left[{}\begin{matrix}\dfrac{-4}{\left(x-1\right)^2}=1\left(vô-nghiệm\right)\\\dfrac{-4}{\left(x-1\right)^2}=-1\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=3\Rightarrow y=4\\x=-1\Rightarrow y=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-1\left(x+1\right)+0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số y=\(2x^4-4x^2-1\) có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết
a) tiếp tuyến vuông góc với đường thẳng \(x-48y+1=0\)
b) tiếp tuyến đi qua \(A\left(1;-3\right)\)
c) tiếp tuyến tiếp xúc voi (C) tại 2 điểm phân biệt
\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được
Đúng 1
Bình luận (0)
Lập phương trình tiếp tuyến của đồ thị hàm số y = -2x^2 biết rằng
a) tiếp tuyến đó đi qua điểm A ( 1;-2)
b) tiếp tuyến đó vuông góc với đường thằng y=-1/3x + 2
c) tiếp tuyến đó song song với đường thẳng y = 4x +2
Tiếp tuyến của đồ thị hàm số \(y=\dfrac{2x-1}{x+1}\) đi qua điểm A(-1;4) có phương trình là :
\(y'=\dfrac{3}{\left(x+1\right)^2}\)
Gọi đường thẳng d qua A có dạng: \(y=k\left(x+1\right)+4\)
d tiếp xúc với (C) khi và chỉ khi: \(\left\{{}\begin{matrix}\dfrac{2x-1}{x+1}=k\left(x+1\right)+4\\\dfrac{3}{\left(x+1\right)^2}=k\end{matrix}\right.\) có nghiệm
\(\Rightarrow\dfrac{2x-1}{x+1}=\dfrac{3\left(x+1\right)}{\left(x+1\right)^2}+4\)
\(\Leftrightarrow2x-1=3+4\left(x+1\right)\)
\(\Leftrightarrow x=-4\)
\(y'\left(-4\right)=\dfrac{1}{3}\) ; \(y\left(-4\right)=3\)
Phương trình tiếp tuyến: \(y=\dfrac{1}{3}\left(x+4\right)+3\)
Đúng 2
Bình luận (0)
Cho hàm số \(y=x^4+x^2+1\) (C). Viết pt tiếp tuyến của đồ thị (C) biết
a) tung độ tiếp điểm bằng 1
b) Tiếp tuyến đi qua điểm \(M\left(-1;3\right)\)
\(y'=4x^3+2x\)
a. \(y=1\Rightarrow x^4+x^2+1=1\Rightarrow x^2\left(x^2+1\right)=0\Rightarrow x=0\Rightarrow y'=0\)
Phương trình tiếp tuyến: \(y=0\left(x-0\right)+1\Leftrightarrow y=1\)
b. \(y'\left(-1\right)=-6\)
Phương trình tiếp tuyến: \(y=-6\left(x+1\right)+3\)
Đúng 2
Bình luận (0)