Trong mặt phẳng Oxy, cho tam giác ABC có S= \(\frac{3}{2}\) , hai đỉnh là A(2;-3), B(3;-2), trọng tâm G nằm trên đường thẳng 3x-y-8=0 . Tìm tọa độ đỉnh C .

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;-3), phương trình đường phân giác trong đỉnh B là x+y-2=0 và phương trình đường trung tuyến hạ từ đỉnh C là x+8y-7=0. Tìm tọa độ các đỉnh B và C của tam giác ABC
goi B(a; b) N( c; d)
\(N\in\left(CN\right)\Rightarrow\)c+8d-7 = 0(1)
N la trung diem AB\(\Rightarrow2c=1+a\left(2\right)\)
2d = -3 +b (3)
B\(\in\left(BM\right)\)\(\Rightarrow\)a+b -2 =0 (4)
tu (1) (2) (3) (4) \(\Rightarrow a=-5;b=7\Rightarrow B\left(-5;7\right)\)
dt (AE) qua vuong goc BM. \(\Rightarrow pt\)(AE):x-y-4 = 0
tọa độ H \(\left\{{}\begin{matrix}x-y-4=0\\x+y-2=0\end{matrix}\right.\Rightarrow H\left(3;-1\right)\);H là trung điểm AE
\(\Rightarrow E\left(5;1\right)\). vì ptdt (BE) cung la ptdt qua (BC):
3x+5y-20 =0
tọa độ C là nghiệm hệ \(\left\{{}\begin{matrix}3x+5y-20=0\\x+8y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{139}{21}\\\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{139}{21};\dfrac{1}{21}\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy Cho tam giác ABC nội tiếp trong đường tròn tâm I; có đỉnh A thuộc đường thẳng d: x + y - 2 = 0, D(2; -1) là chân đường cao của tam giác ABC hạ từ đỉnh A. Gọi điểm E(3; 1) là chân đường vuông góc hạ từ B xuống AI; điểm P(2;1) thuộc đường thẳng AC. Tìm tọa độ các đỉnh của tam giác ABC.
MAT DAY LOP 6,7,8,9 MA DUA LOP 1 , MAT DAY DI MA
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ các đỉnh là \(A(1;1),B(5;2),C(4;4)\). Tính độ dài các đường cao của tam giác ABC.
Ta có: \(\overrightarrow {AB} = \left( {4;1} \right),\overrightarrow {AC} = \left( {3;3} \right),\overrightarrow {BC} = \left( { - 1;2} \right)\)
+) Đường thẳng AB nhận vectơ \(\overrightarrow {AB} = \left( {4;1} \right)\)làm phương trình chỉ phương nên có vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {1; - 4} \right)\) và đi qua điểm \(A(1;1)\), suy ra ta có phương trình tổng quát của đường thẳng AB là:
\(\left( {x - 1} \right) - 4\left( {y - 1} \right) = 0 \Leftrightarrow x - 4y + 3 = 0\)
Độ dài đường cao kẻ từ C chính là khoảng cách từ điểm C đến đường thẳng AB
\(d\left( {C,AB} \right) = \frac{{\left| {4 - 4.4 + 3} \right|}}{{\sqrt {{1^2} + {4^2}} }} = \frac{{9\sqrt {17} }}{{17}}\)
+) Đường thẳng BC nhận vectơ \(\overrightarrow {BC} = \left( { - 1;2} \right)\)làm phương trình chỉ phương nên có vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {2;1} \right)\) và đi qua điểm \(B(5;2)\), suy ra ta có phương trình tổng quát của đường thẳng BC là:
\(2\left( {x - 5} \right) + \left( {y - 2} \right) = 0 \Leftrightarrow 2x + y - 12 = 0\)
Độ dài đường cao kẻ từ A chính là khoảng cách từ điểm A đến đường thẳng BC
\(d\left( {A,BC} \right) = \frac{{\left| {2.1 + 1 - 12} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{{9\sqrt 5 }}{5}\)
+) Đường thẳng AC nhận vectơ \(\overrightarrow {AC} = \left( {3;3} \right)\)làm phương trình chỉ phương nên có vectơ pháp tuyến là \(\overrightarrow {{n_3}} = \left( {1; - 1} \right)\) và đi qua điểm \(A(1;1)\), suy ra ta có phương trình tổng quát của đường thẳng AC là:
\(\left( {x - 1} \right) - \left( {y - 1} \right) = 0 \Leftrightarrow x - y = 0\)
Độ dài đường cao kẻ từ B chính là khoảng cách từ điểm B đến đường thẳng AC
\(d\left( {B,AC} \right) = \frac{{\left| {5 - 2} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{{3\sqrt 2 }}{2}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(4; 3); B(2; 7) và C( - 3; -8). Tìm toạ độ chân đường cao A’ kẻ từ đỉnh A xuống cạnh BC. A. (1 ; -4) B. (-1; 4) C. (1; 4) D. (4; 1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(4; 3); B(2; 7) và C( - 3; -8). Tìm toạ độ chân đường cao A’ kẻ từ đỉnh A xuống cạnh BC.
A. (1 ; -4)
B. (-1; 4)
C. (1; 4)
D. (4; 1)
Gọi A ' x ; y . Ta có A A ' → = x − 4 ; y − 3 B C → = − 5 ; − 15 B A ' → = x − 2 ; y − 7 .
Từ giả thiết, ta có A A ' ⊥ B C B , A ' , C thang hang ⇔ A A ' → . B C → = 0 1 B A ' → = k B C → 2 .
1 ⇔ − 5 x − 4 − 15 y − 3 = 0 ⇔ x + 3 y = 13.
2 ⇔ x − 2 − 5 = y − 7 − 15 ⇔ 3 x − y = − 1.
Giải hệ x + 3 y = 13 3 x − y = − 1 ⇔ x = 1 y = 4 ⇒ A ' 1 ; 4 .
Chọn C.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A( 4; 3); B(2; 7) và C(- 3; -8). Tìm toạ độ chân đường cao A’ kẻ từ đỉnh A xuống cạnh BC? A. A’ (1; -4) B. A’ (-1; 4) C. A’ (1; 4) D.A’ (4; 1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A( 4; 3); B(2; 7) và C(- 3; -8). Tìm toạ độ chân đường cao A’ kẻ từ đỉnh A xuống cạnh BC?
A. A’ (1; -4)
B. A’ (-1; 4)
C. A’ (1; 4)
D.A’ (4; 1)
Gọi A’ (x; y).
Ta có A A ' → = x − 4 ; y − 3 B C → = − 5 ; − 15 B A ' → = x − 2 ; y − 7 .
Từ giả thiết, ta có A A ' ⊥ B C B , A ' , C thang hang ⇔ A A ' → . B C → = 0 1 B A ' → = k B C → 2 .
1 ⇔ − 5 x − 4 − 15 y − 3 = 0 ⇔ x + 3 y = 13.
2 ⇔ x − 2 − 5 = y − 7 − 15 ⇔ 3 x − y = − 1.
Giải hệ x + 3 y = 13 3 x − y = − 1 ⇔ x = 1 y = 4 ⇒ A ' 1 ; 4 .
Chọn C
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tâm đường tròn ngoại tiếp là điểm J(4;0) và phương trình hai đường thẳng lần lượt chứa đường cao và đường trung tuyến từ đỉnh A của tam giác ABC là
d
1
:
x
+
y
–
2
0
và
d
2
:
x
+
...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tâm đường tròn ngoại tiếp là điểm J(4;0) và phương trình hai đường thẳng lần lượt chứa đường cao và đường trung tuyến từ đỉnh A của tam giác ABC là d 1 : x + y – 2 = 0 và d 2 : x + 2 y - 3 = 0 . Tìm tọa độ điểm C, biết B có tung độ dương.
A. C(3;-3).
B. C(7;1).
C. C(1;1).
D. C(-3;-9).
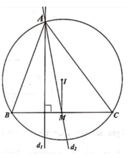
Trong mặt phẳng toạ độ Oxy cho tam giác ABC nội tiếp đường tròn tâm I và D là chân đường phân giác trong đỉnh A của tam giác ABC biết toạ độ các đieemr A(2;6) I(-1/2;1) D(2;-3/2) biết phương trình tổng quát của đường thẳng BC
Trong mặt phẳng cho hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(2; 2), B(1; -3), C(-2; 2). Điểm M thuộc trục tung sao cho \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) nhỏ nhất có tung độ?
Gọi G là trọng tâm tam giác ABC
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{1}{3};y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{1}{3}\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) nhỏ nhất khi \(3MG\) nhỏ nhất
\(\Leftrightarrow M\) là hình chiếu của \(G\) trên trục tung
\(\Leftrightarrow M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\le3MG=1\)
Đẳng thức xảy ra khi \(M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\) Tung độ \(y_M=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Đê - các vuông góc Oxy cho tam giác ABC có AB = AC; \(\widehat{BAC}=90^0\); biết M (1;-1) là trung điểm cạnh BC và \(G\left(\frac{2}{3};0\right)\) là trọng tâm tam giác ABC. Tìm tọa độ các đỉnh A, B, C
Vì G là trọng tâm tam giác ABC, nên ta có :
\(\overrightarrow{MA}=3\overrightarrow{MG}\Leftrightarrow\left(x_A-1;y_A+1\right)=3\left(\frac{2}{3}-1;0+1\right)\Leftrightarrow\begin{cases}x_A-1=1\\y_A+1=3\end{cases}\)
\(\Leftrightarrow A\left(0;2\right)\)
Giả sử \(B\left(x_1;y_1\right);C\left(x_2;y_2\right)\)
Vì M là trung điểm của BC, nên ta có :
\(\begin{cases}x_1+x_2=2\\y_1+y_2=-2\end{cases}\)\(\Leftrightarrow\begin{cases}x_2=2-x_1\\y_2=-2-y_1\end{cases}\)
Vậy \(C\left(2-x_1;-2-y_1\right)\)
Ta có \(\overrightarrow{BA}=\left(-x_1;2-y_1\right);\overrightarrow{CA}=\left(x_1-2;y_1+4\right)\)
Vì \(\widehat{BAC}=90^0\) nên \(\overrightarrow{BA}.\overrightarrow{CA}=0\)
\(\Leftrightarrow-x_1\left(x_1-2\right)+9y_1+4\left(2-y_1\right)=0\)
\(\Leftrightarrow-x^2_1-y^2_1+2x_1-2y_1+8=0\) (1)
Do AB = AC nên \(AB^2=AC^2\)
\(x^2_1+\left(y_1-2\right)^2=2\left(2-x_1\right)^2+\left(4-y_1\right)^2\)
\(\Leftrightarrow-4y_1+4=-4x_1+4+16+8y_1\)
\(\Leftrightarrow x_1=3y_1+4\) (2)
Thay (2) vào (1) ta có :
\(y^2_1+y_1=0\Leftrightarrow\begin{cases}y_1=0\\y_1=-2\end{cases}\)
Từ đó ta có :
\(B\left(4;0\right);C\left(-2;-2\right)\) hoặc \(B\left(-2;-2\right);C\left(4;0\right)\)
Tóm lại ta có :
\(A\left(0;2\right);B\left(4;0\right);C\left(2;-2\right)\) là 3 đỉnh của tam giác cần tìm
(Tam giác kia vẫn là tam giác trên chỉ đổi B và C với nhau)
Đúng 0
Bình luận (0)
Vì G là trọng tâm của tam giác ABC nên ta có :
\(\overrightarrow{MA}=3\overrightarrow{MG}\Leftrightarrow\left(x_A-1;y_A+1\right)=3\left(\frac{2}{3}-1;0+1\right)\Leftrightarrow\begin{cases}x_A-1=-1\\y_A+1=3\end{cases}\)
\(\Leftrightarrow A\left(0;2\right)\)
Ta thấy MA có hệ số góc
\(k=\frac{2-\left(-1\right)}{0-1}=-3\)
Vì \(BC\perp MA\) nên đường thẳng nối BC có hệ số góc là \(\frac{1}{3}\), do đó phương trình của nó là :
\(y=\frac{1}{3}\left(x-1\right)-1\Leftrightarrow x-3y-4=0\)
Mặt khác do :
\(MB=MC=MA=\sqrt{1^2+3^2}=\sqrt{10}\)
Vậy tọa độ của B, C thỏa mãn phương trình đường tròn tâm M, bán kính =\(\sqrt{10}\)
\(\left(x-1\right)^2+\left(y+1\right)^2=10\)
Vậy tọa độ của B, C là nghiệm của hệ phương trình :
\(\begin{cases}x-3y-4=0\\\left(x-1\right)^2+\left(y+1\right)^2=10\end{cases}\)
Giải hệ phương trình ta có các nghiệm (4;0) và (-2;2)
Vậy A(0;2);B(4;0);C(-2;-2) là 3 đỉnh của tam giác cần tìm
Đúng 0
Bình luận (0)