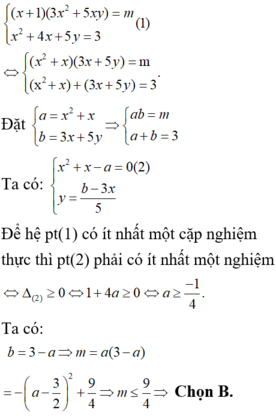Với $x,y$ là số thực thì không tìm được giá trị $x,y$ cụ thể bạn nhé. Bạn xem lại đề.

Lời giải:

Ta có:\(y^2+2\sqrt{2020}y+2022=(y^2+2\sqrt{2020}y+2020)+2=(y+\sqrt{2020})^2+2\geq 2(1)\)

Áp dụng BĐT Bunhiacopxky:

$(\sqrt{x-1}+\sqrt{3-x})^2\leq (x-1+3-x)(1+1)=4$

$\Rightarrow \sqrt{x-1}+\sqrt{3-x}\leq 2(2)$

Từ $(1); (2)\Rightarrow \sqrt{x-1}+\sqrt{3-x}\leq 2\leq y^2+2\sqrt{2020}y+2022$

Dấu "=" xảy ra khi mà: \(\left\{\begin{matrix} \frac{x-1}{1}=\frac{3-x}{1}\\ y+\sqrt{2020}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=2\\ y=-\sqrt{2020}\end{matrix}\right.\)

\(\left(\sqrt{x-1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(x-1+3-x\right)=4\\ \Leftrightarrow\sqrt{x-1}+\sqrt{3-x}\le2\\ y^2+2\sqrt{2020}y+2022=\left(y^2+2y\sqrt{2020}+2020\right)+2\\ =\left(y+\sqrt{2020}\right)^2+2\ge2\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-1=3-x\\y+\sqrt{2020}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\sqrt{2020}\end{matrix}\right.\)

Vậy ...

ĐKXĐ: \(3\ge x\ge1\)

Áp dụng BĐT Bunhiacopski:

\(1\sqrt{x-1}+1\sqrt{3-x}\le\sqrt{\left(1^2+1^2\right)\left(x-1+3-x\right)}=\sqrt{2.2}=2\)

Mặt khác: \(y^2+2\sqrt{2020}y+2022=\left(y+\sqrt{2020}\right)^2+2\ge2\)

Nên để thõa mãn yêu cầu bài toán thì

\(\left\{{}\begin{matrix}\sqrt{x-1}=\sqrt{3-x}\\y+\sqrt{2020}=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\left(tm\right)\\y=-\sqrt{2020}\end{matrix}\right.\)

\(4x^2+4y-4xy+5y^2+1=0\)

\(\Leftrightarrow\left(2x-y\right)^2+\left(2y+1\right)^2=0\)

\(\Leftrightarrow\hept{\begin{cases}x=-\frac{1}{4}\\y=-\frac{1}{2}\end{cases}}\)

\(x^2+5y^2+2y+4xy-3=0\)
\(\Leftrightarrow\)\((x^2+4xy+4y^2)+(y^2+2y+1)=4\)
\(\Leftrightarrow\)\((x+2y)^2+(y+1)^2=4\)
\(\Leftrightarrow\)\((x+2y)^2=4-(y+1)^2\)
\(\Leftrightarrow\)\((x+2y)^2=(2-y-1)(2+y+1)\)
\(\Leftrightarrow\)\((x+2y)^2=(1-y)(3+y)\)
\(Vì \) \((x+2y)^2\geq0\)
\(\Rightarrow\)\((1-y)(3+y)\geq0\)
\(\Rightarrow\)\(\left[\begin{array}{} \begin{cases} 1-y\geq0\\ 3+y\geq0 \end{cases}\\ \begin{cases} 1-y\leq0\\ 3+y\leq0 \end{cases} \end{array} \right.\)
\(\Rightarrow\)\(\left[\begin{array}{} \begin{cases} y\leq1\\ y\geq-3 \end{cases}\\ \begin{cases} y\geq1\text{(Vô lí)}\\ y\leq-3\text{(Vô lí)} \end{cases} \end{array} \right.\)
\(\Rightarrow\)\(-3\leq y\leq1\)
\(\text{Mà y là số nhỏ nhất}\)
\(\Rightarrow\)\(y=-3\)
\(\Rightarrow\)\(x+2.(-3)=0\text{ (Vì }(x+2y)^2\geq0)\)
\(\Rightarrow\)\(x=6\)
\(\text{Vậy cặp số (x,y) thỏa mãn yêu cầu bài toán là: (6;-3)}\)
Nếu mình đúng cho mình xin 1 like nha

VT áp dụng BĐT bu-nhi-a- cop - xki 

Vp đưa về Hđt