tìm m để hai đường thẳng d : y = 5x +m - 3 ; d' : y = 3x + 5 - m cắt nhau tại 1 điểm trên trục tung

Những câu hỏi liên quan
Cho hàm số : y = ( 3m-1)x +m ( m là tham số ) có đồ thị là đường thẳng (d)
a) tìm m để đường thẳng (d) cắt đường thẳng y = 5x - 3
b) Tìm m để đường thẳng ( d ) song song với đường thẳng : y = -4x + 1
Cho đường thẳng y (m+3)-3 (d)
a, Tìm m biết đường thẳng có hệ số góc là 5 .
b, Tim m đề (d) với đường thẳng y=5x-2
c, Với m =-5 . Tính góc tạo bởi đường thẳng và trục ox
d, Tìm m để( d) đi qua A ( 0;5)
Cho hàm số bậc nhất y(m+1)x-3 có đồ thị hàm số là đường thẳng d (m là tham số, m khác -1)a) Tìm m để (d) đi qua E(4; 1) và vẽ đồ thị hàm số với m tìm được.b) Cho (d’): y5x-8 . Tìm m để (d) ⊥(d’).c) Tìm m để đường thẳng (d) cắt đường thẳng y3x-1 tại điểm có hoành độ bằng 2, tìm tọa độ giao điểm.d) Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).
Đọc tiếp
Cho hàm số bậc nhất y=(m+1)x-3 có đồ thị hàm số là đường thẳng d (m là tham số, m khác -1)
a) Tìm m để (d) đi qua E(4; 1) và vẽ đồ thị hàm số với m tìm được.
b) Cho (d’): y=5x-8 . Tìm m để (d) ⊥(d’).
c) Tìm m để đường thẳng (d) cắt đường thẳng y=3x-1 tại điểm có hoành độ bằng 2, tìm tọa độ giao điểm.
d) Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).
a: Thay x=4 và y=1 vào y=(m+1)x-3, ta được:
4(m+1)-3=1
=>4m+4-3=1
=>4m+1=1
hay m=0
b: Để hai đường vuông góc thì 5(m+1)=-1
=>m+1=-1/5
hay m=-6/5
c: Thay x=2 vào y=3x-1, ta được:
\(y=3\cdot2-1=5\)
Thay x=2 và y=5 vào (d), ta được:
2(m+1)-3=5
=>2(m+1)=8
=>m+1=4
hay m=3
Đúng 1
Bình luận (0)
Tìm m để đường thẳng (d) : y = (2m-1)x+3 song song với đường thẳng (d') : y = 5x + 6
Câu 3 (2,0 điểm). Cho hàm số y = (m - 2) x + 2 với m khác 2 có đồ thị là đường thẳng (d)
b) Tìm m để đường thẳng (d) song song với đường thẳng (d1) : y = - 5x + 1
c) Đường thẳng (d) cắt trục Ox tại điểm A, cắt trục Oy tại điểm B. Tìm giá trị của m để diện tích tam giác ABO bằng 1
Em cần gấp ạ
b: Để (d)//(d1) thì m-2=-5 và 2<>1(đúng)
=>m=-3
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m-2\right)x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{-2}{m-2}\end{matrix}\right.\)
=>\(OA=\dfrac{2}{\left|m-2\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)\cdot0+2=2\end{matrix}\right.\)
=>OB=2
\(S_{OAB}=1\)
=>\(\dfrac{1}{2}\cdot OA\cdot OB=1\)
=>\(\dfrac{1}{2}\cdot2\cdot\dfrac{2}{\left|m-1\right|}=1\)
=>\(\left|m-1\right|=2\)
=>\(\left[{}\begin{matrix}m-1=2\\m-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho các đường thẳng (d1): y= (m2+1)x +m và (d2): y=5x+2. Tìm m để hai đường thẳng song song
`(d1) //// (d2) <=> {(a = a'),(b \ne b'):}`
`<=>{(m^2 + 1 = 5),(1 \ne 2\text{ (Luôn đúng)}):}`
`<=> m^2 = 4`
`<=>m = +-2`
Vậy `m = +-2` thì `(d1) //// (d2)`
Đúng 2
Bình luận (2)
TK
(d1)//(d2)⇔{a=a'b≠b'(d1)//(d2)⇔{a=a′b≠b′
⇔{m2+1=51≠2 (Luôn đúng)⇔{m2+1=51≠2 (Luôn đúng)
⇔m2=4⇔m2=4
⇔m=±2⇔m=±2
Vậy m=±2m=±2 thì (d1)//(d2)
Đúng 0
Bình luận (0)
Bài 1: Cho hs y(3m-1)x+m-2 có đths (d)a) Tìm m để hs nghịch biếnb) Tìm m để hs có dạng yaxc) Tìm m để (d) đi qua N(-1;1)d) Tìm m để (d) cắt đường thẳng y 2x-1 tại điểm có hoành độ1 e) Tìm m để (d)// đường thẳng y5x+1f) Tìm m để (d) cât đường thẳng y2x-2020g) Tìm m để (d) vuông góc đường thẳng y1/4x-2019h) Tìm m để (d) cắt đường thẳng y8x-5 tại một điểm thuộc trục tung (trục Oy)Mời các bạn thử sức :P
Đọc tiếp
Bài 1: Cho hs y=(3m-1)x+m-2 có đths (d)
a) Tìm m để hs nghịch biến
b) Tìm m để hs có dạng y=ax
c) Tìm m để (d) đi qua N(-1;1)
d) Tìm m để (d) cắt đường thẳng y =2x-1 tại điểm có hoành độ=1
e) Tìm m để (d)// đường thẳng y=5x+1
f) Tìm m để (d) cât đường thẳng y=2x-2020
g) Tìm m để (d) vuông góc đường thẳng y=1/4x-2019
h) Tìm m để (d) cắt đường thẳng y=8x-5 tại một điểm thuộc trục tung (trục Oy)
Mời các bạn thử sức :P
P/s: Bài này thì không có chắc tại cũng mới học qua
\(a)\) Hàm số trên nghịch biến
\(\Leftrightarrow3m-1< 0\)
\(\Leftrightarrow3m< 1\)
\(\Leftrightarrow m< \frac{1}{3}\)
Vậy \(m< \frac{1}{3}\)thì hàm số trên nghịch biến
\(b)\) Hàm số \(y=\left(3m-1\right)x+m-2\)có dạng \(y=ax\)
\(\Leftrightarrow m-2=0\)
\(\Leftrightarrow m=2\)
\(c)\) VÌ \(n\left(-1;1\right)\in\left(d\right)\Rightarrow\)Thay \(x=-1;y=1\)vào đths
Ta có: \(\left(3m-1\right)\left(-1\right)+m-2=1\)
\(\Leftrightarrow-3m+1+m-2=1\)
\(\Leftrightarrow-2m-1=1\)
\(\Leftrightarrow m=-1\)
Vậy \(m=-1\)
\(d)\) Vì \(\left(d\right)\)cắt đường thẳng \(y=2x-1\)tại điểm có hoành độ \(=1\)
\(\Rightarrow\) Thay \(x=1\)vào hàm số \(y=2x-1\)
Ta có: \(y=2.1-1\)
\(\Leftrightarrow y=2-1=1\)
\(\Leftrightarrow\left(1;1\right)\in\left(d\right)\)
Thay \(x=1;y=1\)vào hàm số \(y=\left(3m-1\right)x+m-2\)
Ta có: \(\left(3m-1\right)1+m-2=1\)
\(\Leftrightarrow3m-1+m-2=1\)
\(\Leftrightarrow4m-3=1\)
\(\Leftrightarrow m=1\)
Vậy \(m=1\)
\(e)\) \(\left(d\right)//\)đường thẳng \(y=5x+1\)
\(\Leftrightarrow\hept{\begin{cases}3m-1=5\\m-2\ne1\end{cases}\Leftrightarrow\hept{\begin{cases}3m=6\\m\ne3\end{cases}\Leftrightarrow}\hept{\begin{cases}m=2\\m\ne3\end{cases}}}\Leftrightarrow m=2\)
Vậy \(m=2\)
\(f)\) \(\left(d\right)\)cắt đường thẳng \(y=2x-2020\)
\(\Leftrightarrow3m-1\ne-2\)
\(\Leftrightarrow3m\ne3\)
\(\Leftrightarrow m\ne1\)
Vậy \(m\ne1\)
\(g)\) \(\left(d\right)\perp\)đường thẳng \(y=\frac{1}{4}x-2019\)
\(\Leftrightarrow\left(3m-1\right).\frac{1}{4}=-1\)
\(\Leftrightarrow\frac{3}{4}m-\frac{1}{4}=-1\)
\(\Leftrightarrow\frac{3}{4}m=-\frac{3}{4}\)
\(\Leftrightarrow m=-1\)
Vậy \(m=-1\)
\(h)\) \(\left(d\right)\)cắt đường thẳng \(y=8x-5\)tại một điểm thuộc trục tung
\(\Leftrightarrow\hept{\begin{cases}3m-1\ne8\\m-2=-5\end{cases}\Leftrightarrow\hept{\begin{cases}3m\ne9\\m=-5+2\end{cases}\Leftrightarrow}\hept{\begin{cases}m\ne3\\m=3\end{cases}}\left(ktm\right)}\)
Vậy không tìm được giá trị \(x\)nào TMĐK
Tìm giá trị của m để: Hai đường thẳng ( d 1 ): 5x – 2y = 3; ( d 2 ): x + y = m cắt nhau tại một điểm trên trục Oy. Vẽ hai đường thẳng này trên cùng một mặt phẳng tọa độ.
Giả sử hai đường thẳng ( d 1 ): 5x – 2y = 3; ( d 2 ): x + y = m cắt nhau tại điểm A(x, y).
Vì giao điểm A nằm trên trục Oy nên x = 0. Suy ra: A(0; y).
Khi đó điểm A(0; y) là nghiệm của hệ phương trình: 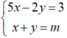
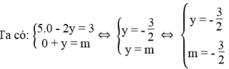
Vậy khi m = - 3/2 thì ( d 1 ): 5x – 2y = 3; (d2): x + y = m cắt nhau tại một điểm trên trục Oy.
Phương trình đường thẳng ( d 2 ): x + y = - 3/2
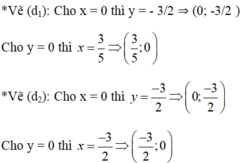
Đồ thị:
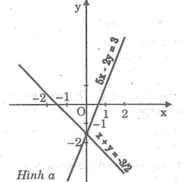
Đúng 0
Bình luận (0)
Tìm m để 2 đường thẳng d:y = 5x+m-3;d':y =3x+5-m cắt nhau tại 1 điểm nằm trên trục tung
\(=>m-3=5-m=>m=4\)
\(5\ne3\) (luôn đúng)
Vậy m=4 thì..............
Đúng 0
Bình luận (0)
Phương trình hoành độ giao điểm :
\(5x+m-3=3x+5-m\)
\(\Leftrightarrow2x=-2m+8\left(1\right)\)
Cắt nhau tại điểm điểm nằm trên trục tung
=> Điểm có hoành độ là 0
\(\left(1\right):-2m+8=0\)
\(\Leftrightarrow m=4\)
Đúng 1
Bình luận (0)





















