trong mặt phẳng Oxy, cho d: 2x+5y-5=0 ; d': 2x+5y+63=0. tìm tọa độ vecto v có phương vuông góc với d để \(T_{\overrightarrow{v}}\)(d)=d'
help pls :(
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình là 2 x + 5 y - 6 = 0 . Tìm tọa độ một vectơ chỉ phương u → của d.
A. u → = ( 2 ; 5 )
B. u → = ( 5 ; 2 )
C. u → = ( 5 ; - 2 )
D. u → = ( - 5 ; - 2 )
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình là 2x+5y-6=0. Tìm tọa độ một vectơ chỉ phương u → của d.
![]()
![]()
![]()
![]()
22. Trong mặt phẳng toạ độ Oxy vectơ nào trong các vectơ sau KHÔNG là vectơ pháp tuyến của đg thẳng d có pt 2x -3y +4=0
A. (4;-6)
B. (-3;2)
C.(-2;3)
D.(2;-3)
23. Trong mặt phẳng toạ độ Oxy , cho đg thẳng d : 4x +3y -23=0 . Điểm nào sau đây ko thuộc d
A. (5;3)
B. (2;5)
C. (-1;9)
D. (8;-3)
24. Trong mặt phẳng toạ độ Oxy , cho đg thẳng d : 3x +5y +2017=0. Tìm mệnh đề sai
A. d có vectơ pháp tuyến n= (3;5)
B. d có vectơ chỉ phương u = (5;-3)
C. d có hệ số góc k=5/3
D. d // vs đg thẳng : 3x +5y =0
22.
Đường thẳng d có 1 vtpt là \(\left(2;-3\right)\)
Do đó \(\left(-3;2\right)\) ko là 1 vtpt của d (vì ko thể biểu diễn thông qua vt (2;-3)
23.
Thay tọa độ 4 điểm vào thì điểm A(5;3) ko thỏa mãn
24.
Đường thẳng d nhận \(\left(3;5\right)\) là 1 vtpt nên nhận \(\left(5;-3\right)\) là 1 vtcp
\(\Rightarrow\) d có hệ số góc là \(-\frac{3}{5}\)
Đáp án C sai
trong mặt phẳng tọa độ oxy cho các đường thẳng (d1): -2x+5y-8=0;(d2): x+2y-5=0;(d3): (m^2-1)x+3y-5-2m=0.xác định m để ba đường thẳng trên là ba đường thẳng phân biệt đồng quy
Tọa độ giao điểm của đường thẳng (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=0\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Để 3 đường thẳng trên đồng qua thì:
\(\left(m^2-1\right)x+3y-5-2m=0\\ \Leftrightarrow\left(m^2-1\right).1+3.2-5-2m=0\\ \Leftrightarrow m^2-1+6-5-2m=0\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=x+2y-5\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y=1\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
Thay x=1 và y=2 vào (d3), ta được:
\(m^2-1+3\cdot2-5-2m=0\)
\(\Leftrightarrow m\left(m-2\right)=0\)
hay \(m\in\left\{0;2\right\}\)
Trong mặt phẳng Oxy, tìm ảnh của đường tháng d / 5 * x - 3y + 15 =0 qua phép Q(0;90°)
A. C. 3x+5y-15=0.
B. 5x - 3v = 0
C.3.5x + 3y = 0
D. 3x+5y+15=0.
35. Trong mặt phẳng tọa độ Oxy , cho hình bình hành ABCD có A(4;-1) , phương trình CD : 2x + 5y +6=0. Viết phương trình cạnh AB.
A. 2x + 5y +3=0
B. 2x +5y -3 =0
C. 4x -y-3=0
D. 2x -5y-3=0
36. Trong mặt phẳng tọA độ Oxy , lập phương trình tổng quát của đg thẳng d , biết d đi qua A(1;3) và song song với trục hoành.
A. x=1
B. y=3
C. x=3
D. y=1
37. Trong mặt phẳng tọa độ Oxy , viết phương trình tổng quát của đg thẳng d , biết rằng d vuông góc với trục hoành đồng thời đi qua A(1;3)
A. y=30
B. y=1
C. x=3
D. x=1
38. Cho 2 đg thẳng d1 : 2x+y-7=0 và d2 : x=-1 + 3t và y=2 + t. Giao điểm của 2 đg thẳng d1 và d2 có tọa độ A(m;n). Tính giá trị P = 2m + n.
A.6
B. 7
C. 8
D.9
39. Trong mặt phẳng tọa độ Oxy , cho điểm M(3;1). Viết phương trình đg thẳng đi qua M và cắt các tia Ox và Oy lần lượt tị A và B sao cho M là trung điểm của AB.
A. 3x + y -10=0
B. x- 3y =0
C. 3x - y -8 = 0
D. x + 3y - 6=0
40. Trong mặt phẳng tọa độ Oxy , tìm hình chiếu N của điểm M (2;-5) lên đg thẳng d : x = -7 + 3t và y = 2 - 4t
A. N( -2/5 ; -34/5)
B. N(2/5 ; 34/5)
C. (-2;-34)
D. ( 2 ;34)
Bài 35:
Do \(AB//CD\) nên đường thẳng AB nhận \(\left(2;5\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x-4\right)+5\left(y+1\right)=0\Leftrightarrow2x+5y-3=0\)
Bài 36:
Do đường thẳng song song trục hoành nên có dạng \(y=a\)
Do đường thẳng qua A(1;3) nên pt là \(y=3\)
Bài 37:
Do thẳng thẳng vuông góc trục hoành nên có dạng \(x=a\)
Đường thẳng qua A(1;3) nên có pt: \(x=1\)
Bài 38:
Thay phương trình d2 vào d1 ta được:
\(2\left(-1+3t\right)+\left(2+t\right)-7=0\)
\(\Leftrightarrow7t-7=0\Rightarrow t=1\)
\(\Rightarrow\left\{{}\begin{matrix}m=-1+3t=2\\n=2+t=3\end{matrix}\right.\)
\(\Rightarrow P=7\)
Bài 39:
Gọi tọa độ A(a;0) và tọa độ B(0;b)
Do M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}\frac{a+0}{2}=3\\\frac{b+0}{2}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=6\\b=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(6;0\right)\\B\left(0;2\right)\end{matrix}\right.\)
Phương trình AB: \(\frac{x}{6}+\frac{y}{2}=1\Leftrightarrow x+3y-6=0\)
Bài 40:
d có 1 vtcp là \(\left(3;-4\right)\)
Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' có 1 vtpt là \(\left(3;-4\right)\)
Phương trình d':
\(3\left(x-2\right)-4\left(y+5\right)=0\Leftrightarrow3x-4y-26=0\)
N là giao của d và d' nên tọa độ N thỏa mãn:
\(3\left(-7+3t\right)-4\left(2-4t\right)-26=0\Rightarrow t=\frac{11}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x_N=-7+3t=-\frac{2}{5}\\y_N=2-4t=-\frac{34}{5}\end{matrix}\right.\) \(\Rightarrow N\left(-\frac{2}{5};-\frac{34}{5}\right)\)
Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình: 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một tâm đối xứng của (H) là:
A. (1;2)
B. (-4;0)
C. (0;19/10)
D. (19/10;0)
Hai đường thẳng d và d’ song song. Điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên bị loại
Tính khoảng cách từ C tới hai đường thẳng d, d’
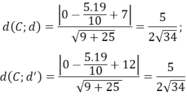
⇒ d(C;d)=d(C;d')=> C là tâm đối xứng
Nhận xét: nếu I là tâm đối xứng của hình gồm hai đường thẳng song song thì I cách đều hai đường thẳng song song đó.
Đáp án C
Trong mặt phẳng Oxy cho hai đường thẳng d: x − 5y + 7 = 0 và d′: 5x – y – 13 = 0. Tìm phép đối xứng qua trục biến d thành d’.
Nhận xét d và d’ không song song nên phép đối xứng trục biến d thành d’ có trục là phân giác của góc tạo bởi d và d’. Phương trình các đường phân giác là:
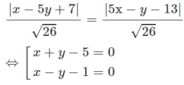
trong mặt phẳng tọa độ Oxy, cho 2 đường thẳng d: 3x+5y=3=0 và d': 3x+5y-5=0. tìm tọa độ vecto v, biết |v|= \(\sqrt{2}\) và \(T_{\overrightarrow{v}}\left(d\right)=d'\)
help pls :(
Chắc pt d là \(3x+5y+3=0\) ?
Gọi \(\overrightarrow{v}=\left(a;b\right)\Rightarrow a^2+b^2=2\) (1)
Gọi \(M\left(-1;0\right)\) là 1 điểm thuộc d
Gọi M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=-1+a\\y_{M'}=b\end{matrix}\right.\) thay vào pt (d') ta được:
\(3\left(-1+a\right)+5b-5=0\)
\(\Leftrightarrow b=\frac{8-3a}{5}\)
Thế vào (1): \(a^2+\left(\frac{8-3a}{5}\right)^2=2\)
\(\Leftrightarrow34a^2-48a+14=0\Rightarrow\left[{}\begin{matrix}a=1\Rightarrow b=1\\a=\frac{7}{17}\Rightarrow b=\frac{23}{17}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}\overrightarrow{v}=\left(1;1\right)\\\overrightarrow{v}=\left(\frac{7}{17};\frac{23}{17}\right)\end{matrix}\right.\)
điểm M đặt bao nhiêu cũng được à bạn? tại thầy mình hay lấy mấy điểm là (0,1) :V