Cho hình vuông ABCD . Biết tổng ba hình vuông nhỏ ở trong là 120 m . Tính cạnh hình vuông ABCD
Ai nhanh cho ba tick
Cho hình vẽ biết tổng chu vi ba hình vuông EFGH IKCG ABCD Là 440cm tính chu vi và diện tích hình vuông abc 440cm tính chu vi và diện tích hình vuông ABCD
Hok có cạnh sao tính được ? Mà muốn tính được phải có hình chứ
Cho hình vuông ABCD. Tính cos A C → , B A → .
A. cos A C → , B A → = 2 2 .
B. cos A C → , B A → = − 2 2 .
C. cos A C → , B A → = 0.
D. cos A C → , B A → = − 1.
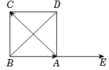
Vẽ A E → = B A → .
Khi đó cos A C → , B A → = cos A C → , A E →
= cos C A E ^ = cos 135 0 = − 2 2 .
Chọn B.
Cho hình vuông ABCD. Tính cos A C → , B A → .
A. cos A C → , B A → = 2 2 .
B. cos A C → , B A → = - 2 2 .
C. cos A C → , B A → = 0.
D. cos A C → , B A → = 1
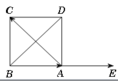
Vẽ A E → = B A → .
Khi đó cos A C → , B A → = cos A C → , A E →
= cos C A E ^ = cos 135 0 = − 2 2 .
Chọn B.
Cho hình vuông ABCD. Tính cos A C → ; B A →
A. -1
B. - 2 2
C. 0
D. 1
cho hình vuông ABCD . trên cạnh AB lấy điểm M tùy í. Dựng hình vuông ngoài hình ABCD hình vuông AMEF trên cạnh AD lấy điểm H và trên tia đối của tia BA lấy điểm K sao cho FH=MK=AB.
CM:EKCH là hình vuông
mk đang cần gấp. mn giúp mk nha
: Ký hiệu (a) là số đo góc a, đặt (CDK)=x
trên tia đối tia AB lấy điểm F sao cho AF = KC
như vậy tam giác ADF bằng tam giác CDK nên góc (ADF)=(CDK)=(KDE)=x
góc (FED)=(EDC)=2x (so le trong)
(FDE)=x+(90-2x)= 90-x
(EFD) = 180 - (FED) - (FDE) = 180 -( 2x) -(90-x) = 90-x = (FDE) vậy tam giác FED cân tại E hay DE =FE = FA +AE =KC + AE dpcm
Cho hình vuông ABCD dựng vào phía trong hình vuông một tam giác đều AMD, dựng ra phía ngoài hình vuông một hình tam giác đều CND. CMR: Ba điểm B,M,N thẳng hàng.
Trong Hình 12, cho biết \(ABCD\) là một hình vuông. Chứng minh rằng:
a) Tứ giác \(EFGH\) có ba góc vuông
b) \(HE = HG\)
c) Tứ giác \(EFGH\) là một hình vuông
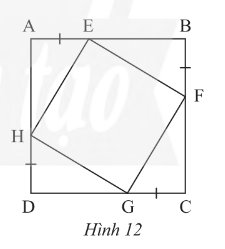
a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) là một góc vuông
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
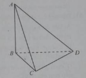
Cho hình tứ diện ABCD có ba cạnh AB, BC, CD đôi một vuông góc.
Đường thẳng AB vuông góc với :
A. (BCD)
B. (ACD)
C. (ABC)
D. (CDI) với I là trung điểm của AB
AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD
Đáp án A
cho hình vuông abcd có cạnh a. Tính vecto BA+ vecto BD
vecto ba+vecto bd
=3a/4
chúc bạn học tốt
