Cho đường tròn đường kính AB = 10 cm; M là trung điểm AC, OM = 3 cm
1. Tính số đo góc ACB.
2. Tính độ dài dây AC.
cho đường tròn O đường kính AD ,dây cung AB .qua B kẻ dây BC vông góc với AD.tính bán kính của đường tròn biết AB=10 cm,BC=12 cm
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
c) Tiếp tuyến tại A của đường tròn (O) cắt BC tại E. Chứng minh:CE.CB = AH. AB
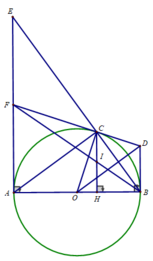
c) Xét tam giác ACB vuông tại C, CH là đường cao nên :
AH.AB = A C 2
Xét tam giác ABE vuông tại A, AC là đường cao nên :
EC.BC = A C 2
⇒ AH.AB = EC.BC
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
b) Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại D. Chứng minh OD ⊥ BC
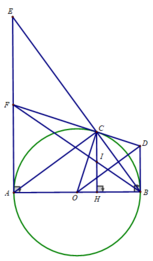
b) DC và DB là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DB
Lại có: OC = OB = R
⇒ OD là đường trung trực của BC hay OD ⊥ BC
1, cho đường tròn (O; 5cm) 1 đường thẳng ik qua A nằm ngoài đường tròn cắt đường tròn tại B và C sao cho AB=BC kẻ đường kính CD độ dài đường thẳng AD là
a.10(cm)
b.12(cm)
c.16(cm)
d.15(cm)
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
a) Chứng minh tam giác ABC vuông. Tính độ dài CH và số đo ∠(BAC) (làm tròn đến độ)
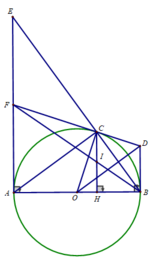
a) Tam giác ABC nội tiếp (O) có AB là đường kính
⇒ ∠(ACB) = 90o
Hay tam giác ABC vuông tại C
Tam giác ABC vuông tại C, CH là đường cao có:
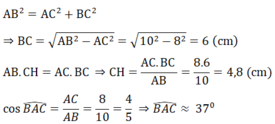
Cho đường tròn tâm O dây AB=10 cm cách O một khoảng bằng 3cm . Tính bán kính đường tròn
Gọi `H` là tđ `AB=>AH=1/2AB=1/2 .10=5(cm)`
Xét `(O)` có: dây `AB` và `H` là tđ không đi qua tâm `O`
`=>OH \bot AB`
Xét `\triangle OHA` vuông tại `H` có:
`AH^2+OH^2=AO^2`
`=>R^2=5^2+3^2`
`=>R=\sqrt{34}(cm)`
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
d) Gọi I là trung điểm của CH. Tia BI cắt AE tại F. Chứng minh: FC là tiếp tuyến của đường tròn (O).
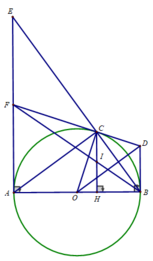
d) Xét tam giác ACB vuông tại C, CH là đường cao nên :
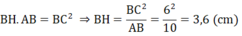
Xét tam giác ABE vuông tại A, AC là đường cao nên :

⇒ EA = 2 FA ⇒ F là trung điểm của EA
Tam giác CEA vuông tại C có CF là trung tuyến
⇒ FC = FA
⇒ ΔFCA cân tại F ⇒ ∠(FCA) = ∠(FAC)
Lại có ΔOCA cân tại O ⇒ ∠(OCA) = ∠(OAC)
⇒ ∠(FCA) + ∠(OCA) = ∠(FAC) + ∠(OAC)
⇔ ∠(FCO) = ∠(FAO) = 90 0
Vậy FC ⊥ CO hay FC là tiếp tuyến của (O)
Cho đường tròn tâm O bán kính 10 cm vẽ đường kính AB vuông góc với dây cung HK biết HK= 8 cm Tính độ dài đoạn thẳng DI
Cho đường tròn tâm O bán kính 10 cm vẽ đường kính AB vuông góc với dây cung HK tại I biết HK = 8 cm. Tính độ dài đoạn thẳng OI
Cho hình vuông ABCD. Vẽ nửa đường tròn đường kính AB và 1/4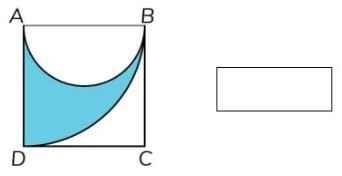
đường tròn bán kính AB. Tính diện tích phần tô đậm biết chu vi đường tròn đường kính AB là 37,68 cm.