Cho tứ giác lồi ABCD. Gọi O là giao điểm của hai đường chéo; I, J là các điểm thỏa mãn các điều kiện IA+ ID= 0, JB +JC = 0; H, H' lần lượt là trực tâm của các tam giác OAB và OCD. Chứng minh rằng hai đường thẳng HH' và IJ vuông góc với nhau.

Những câu hỏi liên quan
cho tứ giác ABCD gọi O là giao điểm của hai đường chéo AC và BD gọi chu vi của tứ giác ABCD là P
Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD . Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và SC. Thiết diện đó là hình gì?
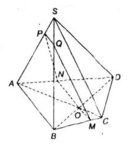
+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.
Đúng 0
Bình luận (0)
Gọi giao điểm hai đường chéo của tứ giác lồi ABCD. Chứng minh rằng đường nối trọng tâm hai tam giác OAB và OCD là vuông góc với đường thẳng nối trực tâm hai tam giác OBC và tam giác ODA
Nhanh đấy . Tưởng tự làm mà :)) lên nhóm lớp tớ giúp cho
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Thiết diện của hình chóp khi cắt bởi mặt phẳng qua O, song song với AB và SC là hình gì?
A. Hình vuông
B. Hình bình hành
C. Hình chữ nhật
D. Hình thang
Đáp án D
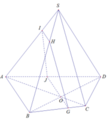
Trong mặt phẳng (ABCD), kẻ đường thẳng d đi qua O và song song với AB
d cắt AD tại J
d cắt BC tại G
Trong mặt phẳng (SBC), kẻ đường thẳng Gx đi qua G và song song với SC; đường thẳng này cắt SB tại H
Trong mặt phẳng (SAB), kẻ đường thẳng y đi qua H và song song với AB
y cắt SA tại I
⇒ IHGJ là thiết diện cần tìm
Xét tứ giác IHGJ có: IH // JG ( // AB )
⇒ IHGJ là hình thang
Đúng 0
Bình luận (0)
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Gọi chu vi tứ giác ABCD là PABCD Chứng minh
a)AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b)Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . gọi chu vi của tứ giác ABCD là PABCD . chứng minh
a) AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b) Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
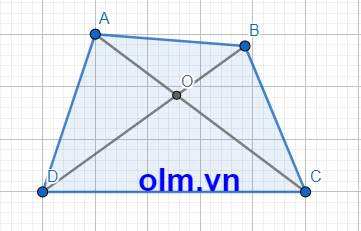
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất. A. OA + OB + OC + OD
AB + BC + CD + DA. B.
A
B
+
B
C
+
C
D
+
D
A
2
O
A
+
O
B
+...
Đọc tiếp
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất.
A. OA + OB + OC + OD < AB + BC + CD + DA.
B. A B + B C + C D + D A 2 < O A + O B + O C + O D .
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
Đáp án cần chọn là:C
+ Xét tam giác OAB ta có OA + OB > AB (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có OC + OD > CD; OB + OC > BC; OA + OD > AD
Cộng vế với vế ta được
OA + OB + OC + OD + OB + OC + OA + OD > AB + BC + CD + AD
⇔ 2(OA + OB + OC + OD) > AB + BC + CD + DA
⇔ OA + OB + OC + OD > A B + B C + C D + D A 2 nên B đúng
+ Xét tam giác ABC có AB + BC > AC (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có BC + CD > BD; CD + DA > AC; AD + DB > BD
Cộng vế với vế ta được
AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD
⇔ 2(AB + BC + CD + DA) > 2(AC + BD)
⇔ AB + BC + CD + DA > AC + BD mà AC + BD = OA + OC + OB + OD nên
OA + OB + OC + OD < AB + BC + CD + DA nên A đúng
Vậy cả A, B đều đúng.
Đúng 0
Bình luận (0)
Cho tứ giác ABCD, gọi O là giao điểm hai đường chéo và I là giao điểm hai cạnh bên AD và BC. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp khi và chỉ khi OA.OC = OB.OD
b) Tứ giác ABCD nội tiếp khi và chỉ khi IA. ID = IB. IC
a) Chúng ta sẽ dùng cách chứng minh phản chứng
Để ABCD là tứ giác nội tiếp thì OA=OB=OC=OD(O là tâm của đường tròn ngoại tiếp tứ giác nội tiếp ABCD vì O là giao điểm của hai đường chéo)
hay \(OA\cdot OC=OB\cdot OD\)(đpcm)
Đúng 0
Bình luận (1)
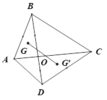
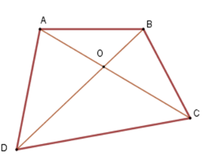
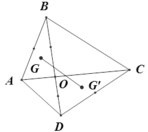
Cho tứ giác ABCD ; gọi O là giao điểm của hai đường chéo AC và BD. Gọi G ; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó
G
G
→
bằng: A. B. C. D.
Đọc tiếp
Cho tứ giác ABCD ; gọi O là giao điểm của hai đường chéo AC và BD. Gọi G ; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó G G ' → bằng:
A. 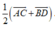
B. 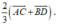
C. ![]()
D. 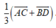
Cho tứ giác ABCD ; gọi O là giao điểm của hai đường chéo AC và BD. Gọi G ; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó
G
G
→
bằng:
Đọc tiếp
Cho tứ giác ABCD ; gọi O là giao điểm của hai đường chéo AC và BD. Gọi G ; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó G G ' → bằng:

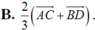
![]()
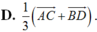
Chọn D.
+ Vì G’ là trọng tâm của tam giác OCD nên 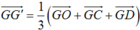 . (1)
. (1)
+ Vì G là trọng tâm của tam giác OAB nên: ![]() (2)
(2)
+ Từ (1) và (2) suy ra: ![]()
Đúng 0
Bình luận (0)