Cho ΔABC đều. Trên tia đối của tia BC lấy điểm D sao cho CD=CB
a. Chứng minh ΔBAD vuông
b. Vẽ AH; CK thứ tự vuông góc với AC; BD. Chứng minh ΔAHC=ΔAKC
c. Chứng minh AH=\(\frac{1}{2}\)AD và AC là đường trung trực đoạn HK
Những câu hỏi liên quan
Cho ΔABC vuông tại A (AB < AC). Vẽ AH ⊥ BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HD = HA.
Chứng minh AE + CD > BC.
Cho ΔABC vuông tại A (AB < AC). Vẽ AH ⊥ BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HD = HA.
a, Chứng minh ΔAHC = ΔDHC
b, Trên HC lấy điểm E sao cho HE = HB. Chứng minh E là trực tâm của ΔADC
c, Chứng minh AE + CD > BC.
a: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
=>ΔAHC=ΔDHC
b: Xet tứ giác ABDE có
H là trung điểm chung của AD và BE
=>ABDE là hình bình hành
=>DE//AB
=>DE vuông góc AC
mà CE vuông góc AD
nên E là trực tâm
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A (AB < AC) có AH là đường cao.
a) Chứng minh: ΔABC đồng dạng ΔHAC và CA^2 = CH.CB.
b) Trên tia đối của tia AB lấy điểm D sao cho góc BCD = 90◦. Vẽ AK ⊥ CD tại K. Chứng minh: ΔCHK đồng dạng ΔCDB.
c) Chứng minh: CK/CD + CH/CB = 1.
Cho ΔABC vuông tại A (AB < AC). Vẽ AH ⊥ BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HD = HA.
a, Chứng minh ΔAHC = ΔDHC
b, Trên HC lấy điểm E sao cho HE = HB. Chứng minh E là trực tâm của ΔADC
c, Chứng minh AE + CD > BC.
* Lưu ý : Đề bài phải có vẽ hình và chứng minh và có cả giả thiết và kết luận.
Cho ΔABC trên tia đối của tia BC lấy điểm D sao cho BD = BA. Trên tia đối của tia CB lấy điểm E sao cho CE = CA. Kẻ BH ⊥ AD, CK ⊥ AE. Chứng minh: a) AH = HD; b) HK // BD
Cho tam giác ABC đều. Lấy điểm E trên tia đối của tia CB sao cho C là trung điểm của đoạn thẳng BE
a. Chứng minh AB=AC=BC=CE
b. Chứng minh tam giác ABE là tam giác vuông
c. Vẽ AH vuông góc BC (H thuộc BC). Trên tia AH lấy điểm D sao cho H là trung điểm của AD. Chứng minh HB=HC
d. Chứng minh C là trọng tâm tam giác ADE
a: Vì ΔABC đều
nên AB=AC=BC
mà BC=CE
nên AB=AC=BC=CE
b: Xét ΔABE có
AC là đường trung tuyến
AC=BE/2
Do đó: ΔABE vuông tại A
c: Ta có; ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh ΔABC = ΔBAD
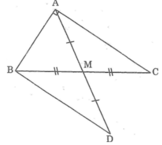
Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
Đúng 0
Bình luận (0)
Cho ΔABC có ba góc nhọn, đường thẳng AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD
a. Chứng minh BC và CB lần lượt là các tia phân giác của các góc ABD và ACD
b. Chứng minh CA = CD và BD = BA
a). Xét tam giác ABH vuông tại H và tam giác DBH vuông tại H có:
AH=DH (GT)
BH là cạnh chung.
=> Tam giác ABH=tam giác DBH (hai cạnh góc vuông).
=> Góc ABH=góc DBH
=> BC là phân giác của góc ABD
Xét tam giác CAH vuông tại H và tam giác CDH vuông tại H có:
AH=DH (GT)
CH là cạnh chung.
=> Tam giác CAH=tam giác CDH (2 cạnh góc vuông)
=> Góc ACH=góc DCH
=> CB là phân giác của góc ACD
b). Vì tam giác ABH=tam giác DBH => BA=BD
Vì tam giác CAH=tam giác CDH => CA=CD
Đúng 0
Bình luận (0)
Bạn tự vẽ hình nha
a.
Xét tam giác ABH và tam giác DBH có:
AH = DH (gt)
AHB = DHB ( = 900)
HB là cạnh chung
=> Tam giác ABH = Tam giác DBH (c.g.c)
=> ABH = DBH (2 góc tương ứng)
=> BH là tia phân giác của ABD
Xét tam giác ACH và tam giác DCH có:
AH = DH (gt)
AHC = DHC ( = 900)
HC là cạnh chung
=> Tam giác ACH = Tam giác DCH (c.g.c)
=> ACH = DCH (2 góc tương ứng)
=> CH là tia phân giác của ACD
b.
CA = CD (Tam giác ACH = Tam giác DCH)
BD = BA (Tam giác ABH = Tam giác DBH)
Đúng 0
Bình luận (0)
Cho ΔABC có góc B = góc C , kẻ AH vuông góc BC, H ∈ BC . Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh:
a) AB = AC
b) ΔABD = ΔACE
c) ΔACD = ΔABE
d) AH là tia phân giác của góc DAE
e) Kẻ BK vuông góc AD, CI vuông góc AE. Chứng minh ba đường thẳng AH, BK, CI cùng đi qua một điểm.
Bài 1: Cho ΔABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho MEMA. chứng minha/ ΔABMΔECMb/ AB//CEBài 2: Cho ΔABC vuông ở A và ABAC. Gọi K là trung điểm của BCa/ Chứng minh : ΔAKBΔAKCb/ Chứng minh: AK vuông góc với BCc/ Từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E. Chứng minh EC//AKBài 3: Cho Δ ABC có ABAC, M là trung điểm của BC. trên tia đối của tia MA lấy điểm D sao cho AM MAa/ Chứng minh ΔABMΔDCMb/ Chứng minh AB//DCc/ Chứng minh AM vuông góc với BCd/ Tìm điều...
Đọc tiếp
Bài 1: Cho ΔABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME=MA. chứng minh
a/ ΔABM=ΔECM
b/ AB//CE
Bài 2: Cho ΔABC vuông ở A và AB=AC. Gọi K là trung điểm của BC
a/ Chứng minh : ΔAKB=ΔAKC
b/ Chứng minh: AK vuông góc với BC
c/ Từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E. Chứng minh EC//AK
Bài 3: Cho Δ ABC có AB=AC, M là trung điểm của BC. trên tia đối của tia MA lấy điểm D sao cho AM= MA
a/ Chứng minh ΔABM=ΔDCM
b/ Chứng minh AB//DC
c/ Chứng minh AM vuông góc với BC
d/ Tìm điều kiện của ΔABC để góc ADC bằng 30o
Bài 4: Cho ΔABC vuông tại A có góc B=30o
a/ Tính góc C
b/ Vẽ tia phân giác của góc C cắt cạnh AB tại D
c/ TRên cạnh CB lấy điểm M sao cho CM=CA. Chứng minh ΔACD=ΔMCD
d/ Qua C vẽ đường thẳng xy vuông góc CA. Từ A kẻ đường thẳng song song với CD cắt xy ở K. Chứng minh : AK=CD
e/ Tính góc AKC.
Bài 5: Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC=Bd
a/ Chứng minh AD=BC
b/ Gọi E là giao điểm AD và BC. Chứng minhΔEAC=ΔEBD
c/ Chứng minh OE là phân giác của góc xOy
Bài 1: Ta có hình vẽ sau:
a)Xét ΔABM và ΔECM có:
BM = CM (gt)
\(\widehat{AMB}=\widehat{EMC}\) (đỗi đỉnh)
MA = ME (gt)
=> ΔABM = ΔACM (c.g.c) (đpcm)
b) Vì ΔABM = ΔECM (ý a)
=> \(\widehat{MAB}=\widehat{MEC}\) (2 góc tương ứng)
mà 2 góc này lại ở vị trí so le trong nên
=> AB // CE (đpcm)
Bài 5: Ta có hình vẽ sau:
a) Vì OA = OB (gt) và AC = BD (gt)
=> OC = OD
Xét ΔOAD và ΔOBC có:
OA = OB (gt)
\(\widehat{O}\) : Chung
OC = OD (cm trên)
=> ΔOAD = ΔOBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)(đpcm)
b) Vì ΔOAD = ΔOBC(ý a)
=> \(\widehat{OBC}=\widehat{OAD}\) và \(\widehat{ODA}=\widehat{OCB}\)
(những cặp góc tương ứng)
Xét ΔEAC và ΔEBD có:
\(\widehat{OBC}=\widehat{OAD}\) (cm trên)
AC = BD (gt)
\(\widehat{ODA}=\widehat{OCB}\) (cm trên)
=> ΔEAC = ΔEBD (g.c.g) (đpcm)
c) Vì ΔEAC = ΔEBD (ý b)
=> EA = EB (2 cạnh tương ứng)
Xét ΔOAE và ΔOBE có:
OA = OB (gt)
\(\widehat{OBC}=\widehat{OAD}\) (đã cm)
EA = EB (cm trên)
=> ΔOAE = ΔOBE (c.g.c)
=> \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
=> OE là phân giác của \(\widehat{xOy}\)
Đúng 0
Bình luận (4)
a) Vì OA = OB (gt) và AC = BD (gt)
=> OC = OD
Xét ΔOAD và ΔOBC có:
OA = OB (gt)
OˆO^ : Chung
OC = OD (cm trên)
=> ΔOAD = ΔOBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)(đpcm)
b) Vì ΔOAD = ΔOBC(ý a)
=> OBCˆ=OADˆOBC^=OAD^ và ODAˆ=OCBˆODA^=OCB^
(những cặp góc tương ứng)
Xét ΔEAC và ΔEBD có:
OBCˆ=OADˆOBC^=OAD^ (cm trên)
AC = BD (gt)
ODAˆ=OCBˆODA^=OCB^ (cm trên)
=> ΔEAC = ΔEBD (g.c.g) (đpcm)
c) Vì ΔEAC = ΔEBD (ý b)
=> EA = EB (2 cạnh tương ứng)
Xét ΔOAE và ΔOBE có:
OA = OB (gt)
OBCˆ=OADˆOBC^=OAD^ (đã cm)
EA = EB (cm trên)
=> ΔOAE = ΔOBE (c.g.c)
=> AOEˆ=BOEˆAOE^=BOE^ (2 góc tương ứng)
=> OE là phân giác của xOyˆ
Đúng 0
Bình luận (0)