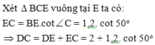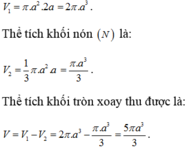cho hình thang ABCD vuông tại A và D. Cho AD=20 ; AC=52 và BC=29. Tính AB

Những câu hỏi liên quan
Cho hình thang ABCD vuông tại A và D;
C
^
50
0
. Biết AB 2; AD 1,2. Tính diện tích hình thang ABCD A.
S
A
B
C
D
2 (đvdt) B.
S
A
B
C
D
3 (đvdt) C. ...
Đọc tiếp
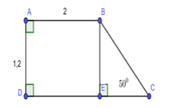
Cho hình thang ABCD vuông tại A và D; C ^ = 50 0 . Biết AB = 2; AD = 1,2. Tính diện tích hình thang ABCD
A. S A B C D = 2 (đvdt)
B. S A B C D = 3 (đvdt)
C. S A B C D = 4 (đvdt)
D. S A B C D = 5 2 (đvdt)
Cho hình thang ABCD vuông tại A và D, cạnh ABADa và DC2a. Thể tích khối tròn xoay sinh ra khi hình thang ABCD quay quanh trục AD là A.
5
πa
3
3
B.
7
πa
3
3
C.
8
πa
3
3...
Đọc tiếp
Cho hình thang ABCD vuông tại A và D, cạnh AB=AD=a và DC=2a. Thể tích khối tròn xoay sinh ra khi hình thang ABCD quay quanh trục AD là
A. 5 πa 3 3
B. 7 πa 3 3
C. 8 πa 3 3
D. 4 πa 3 3
Cho hình thang abcd vuông tại a và d cho biết ab=12cm cd=18cm,ad=8cm.Tính diện tích hình thang abcd, tỉ số phần trăm diện tích tam giác bcd và diện tích hình thang abcd
ABCD là hình thang vuông tại A và D
=>\(S_{ABCD}=\dfrac{1}{2}\cdot AD\cdot\left(BA+CD\right)=\dfrac{1}{2}\cdot8\cdot\left(12+18\right)=4\cdot30=120\left(cm^2\right)\)
Diện tích tam giác ABD là:
\(S_{ABD}=\dfrac{1}{2}\cdot AB\cdot AD=\dfrac{1}{2}\cdot12\cdot8=4\cdot12=48\left(cm^2\right)\)
Ta có: \(S_{ABD}+S_{BDC}=S_{ABCD}\)
=>\(S_{BDC}+48=120\)
=>\(S_{BDC}=72\left(cm^2\right)\)
=>\(\dfrac{S_{BCD}}{S_{ABCD}}=\dfrac{72}{120}=\dfrac{3}{5}=60\%\)
Đúng 1
Bình luận (0)
Cho hình thang vuông ABCD vuông tại A và D, cho AB= 1/3 CD. Kéo dài BC và AD cắt nhau tại M. Diện tích hình thang ABCD= 64 cm2. Tính diện tích tam giác MAB
Xét ΔMCD có AB//CD
nên ΔMAB~ΔMDC
=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{AB}{CD}\right)^2=\dfrac{1}{9}\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot S_{MDC}\)
Ta có: \(S_{MAB}+S_{ABCD}=S_{MDC}\)
=>\(S_{ABCD}=S_{MDC}-\dfrac{1}{9}\cdot S_{MDC}=\dfrac{8}{9}\cdot S_{MDC}\)
=>\(S_{MDC}=64:\dfrac{8}{9}=72\left(cm^2\right)\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot72=8\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 3 cm và CD = 4cm. Tính AC?
A. 3cm
B. 4cm
C. 3,5cm
D. 5cm
Do tứ giác ABCD là hình thang vuông nên D ^ = 90 ° . Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng định lí Pi-ta-go vào tam giác ACD vuông tại D ta có:
A C 2 = A D 2 + D C 2 = 3 2 + 4 2 = 25
Suy ra A C = 5 c m
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD vuông tại A và D, có AB = 6cm; DC = 9cm ; BC = 5cm. Tính AD?
A. 3cm
B. 4cm
C. 5cm
D. 6cm
Cho hình thang ABCD vuông tại A và D, ADCDa, AB2a. Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là:
Đọc tiếp
Cho hình thang ABCD vuông tại A và D, AD=CD=a, AB=2a. Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là:
![]()
![]()
![]()
![]()
Cho hình thang ABCD vuông tại A và D,
A
D
C
D
a
,
A
B
2
a
. Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là: A.
5
πa
3
3
B.
7
πa
3...
Đọc tiếp
Cho hình thang ABCD vuông tại A và D, A D = C D = a , A B = 2 a . Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là:
A. 5 πa 3 3
B. 7 πa 3 3
C. 4 πa 3 3
D. πa 3
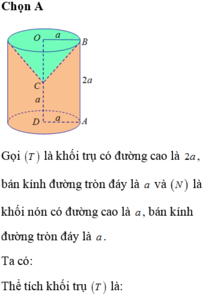
Chọn đáp án A
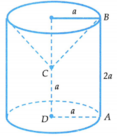
Gọi (T) là khối trụ có đường cao là 2a, bán kính đường tròn đáy là a và (N) là khối nón có đường cao là a, bán kính đường tròn đáy là a
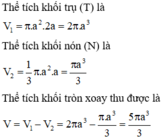
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD tại A và D; ADCDa; ABa Quay hình thang ABCD xung quanh đường thẳng CD. Thể tích khối tròn xoay thu được là A.
5
π
a
3
3
B.
7
π
a
3
3
C.
4
π...
Đọc tiếp
Cho hình thang vuông ABCD tại A và D; AD=CD=a; AB=a Quay hình thang ABCD xung quanh đường thẳng CD. Thể tích khối tròn xoay thu được là
A. 5 π a 3 3
B. 7 π a 3 3
C. 4 π a 3 3
D. π a 3
Đáp án A
Gọi V là thể tích của khối tròn xoay cần tính, khi đó V = V 1 − V 2 với
V1 là thể tích khối trụ có chiều cao h 1 = A B , bán kính R = A D → V 1 = π R 2 h 1 = 2 π a 3
V 2 là thể tích khối trụ có chiều cao h 1 = A B − C D , bán kính R = A D → V 2 = 1 3 π r 2 h 2 = π a 3 3
Vậy thể tích cần tính là V = V 1 − V 2 = 2 π a 3 − π a 3 3 = 5 π a 3 3
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD tại A và D, AD CD a, AB 2a. Quay hình thang ABCD xung quanh đường thẳng CD. Thể tích khối tròn xoay thu được là A.
5
πa
3
3
B.
7
πa
3
3
C.
4
πa...
Đọc tiếp
Cho hình thang vuông ABCD tại A và D, AD = CD = a, AB = 2a. Quay hình thang ABCD xung quanh đường thẳng CD. Thể tích khối tròn xoay thu được là
A. 5 πa 3 3
B. 7 πa 3 3
C. 4 πa 3 3
D. πa 3