MH ơ đâu vậy

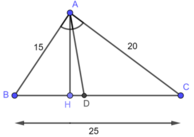
a) Trong tam giác ABC, ta có: AD là đường phân giác của:

Mà AB = 15cm và AC = 20cm ( gt )

Nên \(\dfrac{DC}{DB}\)

( Tính chất tỉ lệ thức đã học ở lớp 7 )

b) Kẻ 

Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD

\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD

⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)

Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)

⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)

Ta có tam giác ABC vuông tại A => BC² = AB² + AC²

=> AC² = BC² - AB² = 25² - 20² = 625 - 400 = 225

=> AC = 15

Vì tam giác ABC vuông tại A => BC^2=AB^2+AC^2 ( theo định lí Pi-ta-go)

                                         <=>   AC^2=BC^2-AB^2

                                         <=>  AC^2=625-400

                                        <=>  AC^2=225

                                          <=>  AC=15

a) Xét tam giác ABC có:

BD là tia phân giác \(\widehat{BAC}\)

\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)

 \(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)

\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)

b) Kẻ đường cao AH của tam giác ABC

\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)

a: Xét ΔABC có 

AD là đường phân giác ứng với cạnh BC

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)

hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)

mà BD+CD=25cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)

Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)

Tam giác AHB vuông tại H => Áp dụng định lý pitago ta có :

AB² = AH² + HB² => HB² = AB² - AH² = 25² - 24² = 625 - 576 = 49 = 7²

=> HB = 7

Tam giác AHC vuông tại H => Áp dụng định lý pitago ta có :

AC² = CH² + AH² => CH² = AC² - AH² = 26² - 24² = 676 - 576 = 100 = 10²

=> CH = 10

=> BC = HB + CH = 7 + 10 = 17 (cm)

Vậy BC = 17 (cm)

Giải:

Áp dụng định lý Py-ta-go vào tam giác AHB (tam giác AHB vuông tại H)

=> AB² = AH² + HB² 

=> HB² = AB² - AH² 

=> HB² = 25² - 24²

=> HB = 625 - 526 = 49 = 7² 

=> HB = 7

Áp dụng định lý Py-ta-go và tam giác AHC (tam giác AHC vuông H)

=> AC² = AH² + HC²

=> HC² = AC² - AH²

=> HC² = 26² - 24²

=> HC  = 676 - 576 = 100 = 10²

=> HC = 10

=> BC = BH + HC 

     BC = 7 + 10 = 17 (cm)

Vậy BC = 17 cm.

\(BC=BH+CH=25+144=169\left(cm\right)\)

Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH có:

\(AH^2=HB.HC=25.144\Rightarrow AH=\sqrt{3600}=60\left(cm\right)\)

\(AB^2=BH.BC=25.169=4225\Rightarrow AB=\sqrt{4225}=65\left(cm\right)\)

\(AC^2=CH.CB=144.169=24336\Rightarrow AC=\sqrt{24336}=156\left(cm\right)\)

a. ta có \(\hept{\begin{cases}\frac{DB}{DC}=\frac{AB}{AC}=\frac{10}{25}=\frac{2}{5}\\BD+DC=BC=30\end{cases}\Rightarrow\hept{\begin{cases}DB=\frac{60}{7}\\DC=\frac{150}{7}\end{cases}}}\)

mà \(\frac{DE}{AB}=\frac{CD}{CB}=\frac{5}{7}\Rightarrow DE=\frac{50}{7}cm\)

b.ta có \(\frac{S_{ABD}}{S_{ABC}}=\frac{BD}{BC}=\frac{2}{7}\Rightarrow S_{ABD}=\frac{120.2}{7}=\frac{240}{7}cm^2\Rightarrow S_{ACD}=S_{ABC}-S_{ABD}=\frac{600}{7}\)

mà 

\(\frac{S_{AED}}{S_{ADC}}=\frac{AE}{AC}=\frac{BD}{BC}=\frac{2}{7}\Rightarrow S_{AED}=\frac{600}{7}\frac{.2}{7}=\frac{1200}{49}cm^2\Rightarrow S_{CDE}=S_{ACD}-S_{AED}=\frac{3000}{49}\)