cho P:y=x2+4x+1 và đường thẳng d:y=2x+3m-1
Tìm m để d và P cắt nhau tại hai điểm sao cho
a; AB=2√5
b; tam giác OAB cân
Gọi S là tập hợp tất các giá trị thực của tham số m để đường thẳng d : y = m x cắt parabol P : y = - x 2 + 2 x + 3 tại hai điểm phân biệt A và B sao cho trung điểm I của đoạn thẳng AB thuộc đường thẳng ∆ : y = x - 3 . Tính tổng tất cả các phần tử của S.
A. 2
B. 1
C. 5
D. 3
Phương trình hoành độ giao điểm: - x 2 + 2 x + 3 = m x ⇔ x 2 + m - 2 x - 3 = 0 1
Dễ thấy (1) luôn có 2 nghiệm phân biệt vì a c = 1 . - 3 = - 3 < 0
Khi đó (d) cắt (P) tại hai điểm phân biệt A x 1 ; m x 1 , B x 2 ; m x 2 , với x 1 , x 2 là nghiệm phương trình (1). Theo Viét, có: x 1 + x 2 = 2 - m , x 1 x 2 = - 3 x 1 x 2 = - 3
I là trung điểm
A B ⇒ I = x 1 + x 2 2 ; m x 1 + m x 2 2 = 2 − m 2 ; − m 2 + 2 m 2
Mà I ∈ ( Δ ) : y = x − 3 ⇒ − m 2 + 2 m 2 = 2 − m 2 − 3 ⇔ m 2 − 3 m − 4 = 0
⇔ m = − 1 = m 1 m = 4 = m 2 ⇒ m 1 + m 2 = 3
Đáp án cần chọn là: D
Cho P : y = x 2 + 2 x - 3 và d : y = m x - 4 - 2 . Tìm m để d cắt tại hai điểm A x 1 ; y 1 , B x 2 ; y 2 sao cho biểu thức P = 2 x 1 2 + x 2 2 + 9 x 1 x 2 + 2014 đạt giá trị nhỏ nhất
A. m > 10 + 2 23
B. m > -3
C. m = -3
D. m < 10 - 2 23
Đáp án C
Tọa độ giao điểm của hai đồ thị là nghiệm của phương trình

Cho p:y=x^2 và d:y=(2m+1)x-2m.tìm m để d cắt p tại hai điểm phân biệt M(x1,y1),N(x2,y2) sao cho y1+y2-x1x2
Phương trình hoành độ giao điểm của \(\left(d\right),\left(P\right)\) là : \(x^2=\left(2m+1\right)x-2m\)
hay : \(x^2-\left(2m+1\right)x+2m=0\left(I\right)\).
Do, \(\left(d\right)\cap\left(P\right)\) tại hai điểm phân biệt nên phương trình \(\left(I\right)\) có hai nghiệm phân biệt khi \(\Delta=b^2-4ac>0\)
Hay : \(\left[-\left(2m+1\right)\right]^2-4.1.2m>0\)
\(\Leftrightarrow4m^2+4m+1-8m>0\)
\(\Leftrightarrow\left(2m-1\right)^2>0\Rightarrow m\ne\dfrac{1}{2}\).
Theo định lí Vi-ét : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(2m+1\right)}{1}=2m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{2m}{1}=2m\end{matrix}\right.\)
Theo đề bài : \(y_1+y_2-x_1x_2=1\left(II\right)\)
Do các điểm trên thuộc \(\left(P\right)\) nên \(\left\{{}\begin{matrix}y_1=x_1^2\\y_2=x_2^2\end{matrix}\right.\).
Khi đó, ta viết lại phương trình \(\left(II\right)\) thành : \(x_1^2+x_2^2-x_1x_2=1\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=1\)
\(\Rightarrow\left(2m+1\right)^2-3.2m=1\)
\(\Leftrightarrow4m^2+4m+1-6m=1\)
\(\Leftrightarrow4m^2-2m=0\)
\(\Leftrightarrow2m\left(2m-1\right)=0\Leftrightarrow\left[{}\begin{matrix}2m=0\\2m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
Vậy : \(m=0\).
Cho P:y= 1/2x^2 và d:y= 2x-m^2 -1.
Tìm m để d cắt p tại 2 điểm có hoành độ x1, x2 thỏa mãn 1/x1 =1/ |x2| +1/2
Pt hoành độ giao điểm:
\(-\dfrac{1}{2}x^2=2x-m^2-1\Leftrightarrow x^2+4x-2\left(m^2+1\right)=0\)
\(ac=-2\left(m^2+1\right)< 0\) ; \(\forall m\Rightarrow\) (d) luôn cắt (P) tại 2 điểm có hoành độ trái dấu
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-4\\x_1x_2=-2\left(m^2+1\right)\end{matrix}\right.\)
Ta có: \(\dfrac{1}{x_1}=\dfrac{1}{\left|x_2\right|}+\dfrac{1}{2}>0\Rightarrow x_1>0\Rightarrow x_2< 0\Rightarrow\dfrac{1}{\left|x_2\right|}=-\dfrac{1}{x_2}\)
Do đó:
\(\dfrac{1}{x_1}=\dfrac{1}{\left|x_2\right|}+\dfrac{1}{2}\Leftrightarrow\dfrac{1}{x_1}=-\dfrac{1}{x_2}+\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{1}{2}\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{-4}{-2\left(m^2+1\right)}=\dfrac{1}{2}\Leftrightarrow m^2+1=4\)
\(\Leftrightarrow m^2=3\Rightarrow m=\pm\sqrt{3}\)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : y = m x + 5.
b) Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol P : y = x 2 tại hai điểm phân biệt có hoành độ lần lượt là x 1 , x 2 (với x 1 < x 2 ) sao cho x 1 > x 2 .
Xét phương trình hoành độ giao điểm của (d) và (P):
x 2 = m x + 5 ⇔ x 2 − m x − 5 = 0 .
Ta có tích hệ số a c = − 5 < 0 nên phương trình hoành độ giao điểm luôn có 2 nghiệm phân biệt với mọi m hay thẳng (d) cắt parabol (P) tại hai điểm phân biệt với mọi m.
Theo hệ thức Vi-ét ta có x 1 + x 2 = m x 1 x 2 = − 5 Ta có:
x 1 > x 2 ⇔ x 1 2 > x 2 2 ⇔ x 1 2 − x 2 2 > 0 ⇒ x 1 + x 2 x 1 − x 2 > 0
Theo giả thiết: x 1 < x 2 ⇔ x 1 − x 2 < 0 do đó x 1 + x 2 < 0 ⇔ m < 0 .
Vậy thỏa mãn yêu cầu bài toán.
Cho parapol p:y=x2 và đường thẳng D:y=mx+m+1
1.tìm m để đường thẳng D cắt p tại hai điểm phân biệt A,B
2.gọi x1,x2 là hoành độ của A và B.tìm m sao cho |x1-x2|=2
Cho (P): y=-x^2 và đường thẳng d:y=2x+m-1. Tìm m để d cắt (P) tại hai điểm phân biệt A(x1;y1), B(x2;y2) mà x1y2 - x2y2 - x1x2= -4
Tất cả các giá trị thực của tham số m để đường thẳng d:y=2x+m cắt đồ thị hàm số y = 2 x - 4 x - 1 tại hai điểm phân biệt A và B sao cho 4 S ∆ I A B = 15 , với I là giao điểm của hai đường tiệm cận của đồ thị (C) là
A. m = ± 5
B. m=0
C. m=5
D. m=-5
Phưng trình hoành độ giao điểm:
![]()
![]()
![]()
Đường thẳng d cắt đồ thị (C) tại 2 điểm phân biệt
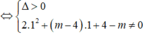
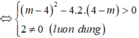
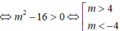
Khi đó, (*) có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
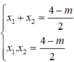
Tọa độ hai giao điểm là:
![]()
![]()
= 5 . x 1 - x 2 2
![]()
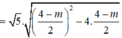
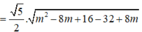
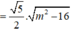
Giao điểm của hai đường tiệm cận của đồ thị (C) là: I(1;2)
Ta có: ![]()
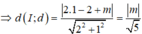
Ta có:
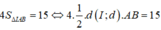
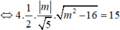
![]()
 (thỏa mãn)
(thỏa mãn)
Chọn đáp án A.
Cho P:y=x^2,d:y=ax+b.
a)Tìm điểm M(x0;y0) thuộc parabol P sao cho khoảng cách từ M đến hai trục tọa độ bằng nhau
b)Xác định a,b để đường thẳng d đi qua điểm A(1;1) và d cũng là tiếp tuyến của P
\(a\text{) Gọi }M\left(m;m^2\right)\in P\)
\(d\left(M;Ox\right)=d\left(M;Oy\right)\Leftrightarrow\left|x_M\right|=\left|y_M\right|\)\(\Leftrightarrow\left|m\right|=\left|m^2\right|\Leftrightarrow m^2=m\text{ hoặc }m^2=-m\)
\(\Leftrightarrow m^2-m=0\text{ hoặc }m^2+m=0\)
\(\Leftrightarrow m=0\text{ hoặc }m=1\text{ hoặc }m=-1\)
\(\text{Kết luận: }M\left(0;0\right)\text{ hoặc }M\left(1;1\right)\text{ hoặc }M\left(-1;1\right)\)
\(b\text{) }A\in d\Rightarrow a+b=1\text{ (1)}\)
\(\text{Phương trình hoành độ giao điểm của }P\text{ và }d\text{ là: }x^2=ax+b\)
\(\Leftrightarrow x^2-ax-b=0\text{ (*)}\)
\(d\text{ là tiếp tuyến của }P\Leftrightarrow d\text{ giao }P\text{ tại 1 điểm duy nhất }\Leftrightarrow\left(\text{*}\right)\text{ có nghiệm kép }\)
\(\Leftrightarrow\Delta=a^2+4b=0\text{ (2)}\)
\(\left(1\right)\Leftrightarrow b=1-a;\text{ thay vào (2) ta được: }a^2+4\left(1-a\right)=0\)
\(\Leftrightarrow a^2-4a+4=0\Leftrightarrow\left(a-2\right)^2=0\Leftrightarrow a=2\)
\(\Rightarrow b=-1\)
\(\text{Vậy }a=2;\text{ }b=-1\)