Tập nghiệm của phương trình ( x 2 – x – 1)( x 2 – x + 1) = 3 là
A. S = {-1; -2}
B. S = {1; 2}
C. S = {1; -2}
D. S = {-1; 2}
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Các khẳng định sau đây đúng hay sai:
a. Phương trình 4 x - 8 + 4 - 2 x x 2 + 1 = 0 có nghiệm x = 2.
b. Phương trình x + 2 2 x - 1 - x - 2 x 2 - x + 1 = 0 có tập nghiệm S = {-2; 1}
c. Phương trình x 2 + 2 x + 1 x + 1 = 0 có nghiệm x = - 1
d. Phương trình x 2 x - 3 x = 0 có tập nghiệm S = {0; 3}
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 
Câu 1 : Phương trình nào trong các phương trình dưới đây là phương trình bậc nhất ?
A. 7 - x - 3x2 = x - 3x2 B. 4 - x = - ( x - 1)
C. 3 - x + x2 = x2 - x - 2 D. ( x - 3 )( x + 5 ) = 0
Câu 2 : Phương trình nào dưới đây có tập nghiệm là S = {3; -1}
A. ( x + 3)(x - 1) = 0 B. x2 + 3x + 2 = 0
C. x( x – 3)(x + 1)2 = 0 D. ( x – 3)(x + 1) = 0
Câu 3 : Phương trình nào dưới đây có vô số nghiệm ?
A. ( x + 3 )( x2 + 5 ) = 0. B. x2 = - 9
C. x3 = - 27 D. 5x - 3 + 3x = 8x - 3
Câu 4 : Phương trình - 2x2 + 11x - 15 = 0 có tập nghiệm là:
A. 3 B. C . D.
Câu 5. Điều kiện xác định của phương trình là:
A hoặc x ≠ -3 B.; C. và x ≠ - 3; D. x ≠ -3
Câu 6. Biết và CD = 21 cm. Độ dài của AB là:
A. 6 cm B. 7 cm; C. 9 cm; D. 10 cm
Câu 7. Cho tam giác ABC, AM là phân giác (hình 1). Độ dài đoạn thẳng MB bằng:
A. 1,7 B. 2,8 C. 3,8 D. 5,1
Câu 8. Trong Hình 2 biết MM' // NN', MN = 4cm, OM’ = 12cm và M’N’ = 8cm. Số đo của đoạn thẳng OM là:
A. 6cm; B. 8cm; C. 10cm; D. 5cm
Hình 1 Hình
1.B
2.D
3.B
4;5;6;7;8( bạn sửa lại đề nhé )
Đúng ghi Đ, sai ghi S. Điền vào chỗ chấm:
a) Phương trình 2 x + 5 = 11 và phương trình 7 x - 2 = 19 là hai phương trình tương đương. ....
b) Phương trình 3 x - 9 = 0 v à x 2 - 9 = 0 là hai phương trình tương đương. ....
c) Phương trình 0 x + 2 = x + 2 - x có tập nghiệm là S = {2} ....
d) Phương trình ( 2 x - 3 ) ( 3 x + 1 ) = 0 có tập nghiệm là S = 3 / 2 ; - 1 / 3 . . . .
Câu 1: [1] Gọi S là tập nghiệm của phương trình ( x+2)(2x-1)(x-3) = 0. Khẳng định nào sau đây sai?
A. -2 ∈ S B. 3 ∈ S C. 2 ∈ S D. \(\dfrac{1}{2}\) ∈ S
Ta có tập nghiệm của phương trình là:
\(\left(x+2\right)\left(2x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\2x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Tập hợp S là:
\(S=\left\{-2;\dfrac{1}{2};3\right\}\)
Lần lược các phương án:
A. \(-2\in S\) (đúng)
B. \(3\in S\) (đúng)
C. \(2\in S\) (Sai)
D. \(\dfrac{1}{2}\in S\) (Đúng)
⇒ Chọn C
Câu 2. Tập nghiệm của phương trình √(x ^ 2 - x + 1) = √(x ^ 2 + 2x + 4) là A. S = {1} . B. S = {0} C. S = mathcal O . D. S = {-1} . Giúp vs bạn ơi:(
Phương trình \(\sqrt{2-f\left(x\right)}=f\left(x\right)\) có tập nghiệm A = {1;2;3}. Phương trình \(\sqrt{2.g\left(x\right)-1}+\sqrt[3]{3.g\left(x\right)-2}=2.g\left(x\right)\) có tập nghiệm là B = {0;3;4;5} . Hỏi tập nghiệm của phương trình \(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)+1=f\left(x\right)+g\left(x\right)\)
có bao nhiêu phần tử?
A.1
B.4 C.6 D.7
\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử
Gọi S là tập nghiệm của phương trình 2 ( 2 x - 1 ) - 5 . 2 ( x - 1 ) + 3 = 0 . Tìm S.
A. S = {1; log23 }
B. S = {0; log 2 3 }
C. S = {1; log 3 2 }
D. S = {1}
Đáp án A
Phương pháp:
Đặt ẩn phụ, đưa về phương trình bậc hai một ẩn. Giải phương trình và suy ra ẩn t.
Cách giải:
![]()
![]()
Phương trình đã cho trở thành
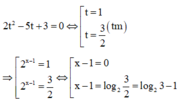
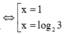
![]()
Câu 4. Tập nghiệm của phương trình: x(x+ 1) = 0 là:
A. S = {0}. B. S = {0;1}. C. S = {–1}. D. S = {0; –1}.
Câu 5. Phương trình nào sau đây có 1 nghiệm:
A. x2 – 3x = 0. B. (x + 2)(x2 + 1) = 0.
C. x (x – 1) = 0. D. 2x + 1 = 1 + 2x.
Câu 6. Phương trình 2x – 3 = 1 tương đương với phương trình nào:
A. x2 – x = 0. B. x2 – 1 = 0.
C. ![]() . D.
. D. ![]() .
.
Câu 7. ![]() là nghiệm của phương trình:
là nghiệm của phương trình:
A.![]() . B.
. B.![]() . C.
. C.![]() . D.
. D.![]() .
.
Câu 8. Phương trình ![]() có tập nghiệm S là :
có tập nghiệm S là :
A. ![]() . B. S = {- 4}. C. S = {4;-4}. D. S = {4}.
. B. S = {- 4}. C. S = {4;-4}. D. S = {4}.
Câu 9. Ở hình 2, x = ?
A. 9cm. B. 6cm. C. 1cm. D. 3cm.

Câu 10. Cho ![]() ABC có AD là đường phân giác (D
ABC có AD là đường phân giác (D![]() BC), biết
BC), biết ![]() và CD = 15cm. Độ dài đoạn BD là:
và CD = 15cm. Độ dài đoạn BD là:
A. 5cm. B. 10cm. C. 30cm. D. 45cm.

Câu 11. ![]()
![]()
![]() theo tỉ số k thì
theo tỉ số k thì ![]() ~
~ ![]() theo tỉ số
theo tỉ số
A. – k. B. k2. C. ![]() . D. – k2.
. D. – k2.
Câu 12. ![]()
![]()
![]() theo tỉ số là 2 thì tỉ số diện tích của
theo tỉ số là 2 thì tỉ số diện tích của ![]() và
và ![]() là:
là:
A. 2. B. 4. C. 1/2. D. 1/4.
4D
5B
Các câu còn lại bạn ghi lại đề nha bạn, đề bị lỗi rồi
Gọi S là tập nghiệm của phương trình log 5 ( x + 1 ) + log 5 ( x - 3 ) = 1 Tìm S
A. S = - 2 ; 4
B. S = - 1 + 13 2 ; - 1 - 13 2
C. S = 4
D. S = - 1 + 13 2