Cho tam giác ABC vuông cân tại A(2; -1). Cạnh huyền BC : x +3y - 2 = 0. Viết phương trình 2 cạnh góc vuông
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ các tam giác ABD vuông cân tại A, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. CMR: Tứ giác BDEC là hình thang cân
Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng AECB là hình thang vuông
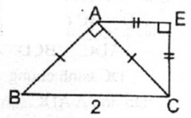
Tam giác ABC vuông cân tại A
⇒ ∠ (ACB) = 45 0
Tam giác EAC vuông cân tại E
⇒ ∠ (EAC) = 45 0
Suy ra: ∠ (ACB) = ∠ (EAC)
⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác AECB là hình thang có ∠ E = 90 0 . Vậy AECB là hình thang vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng tứ giác BDEC là hình thang cân.
Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Tính các góc và các cạnh của hình thang AECB
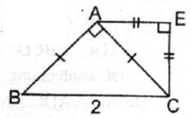
∠ E = ∠ (ECB) = 90 0 , ∠ B = 45 0
∠ B + ∠ (EAB) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (EAB) = 180 0 - ∠ B = 180 0 – 45 0 = 135 0
Tam giác ABC vuông tại A. Theo định lí Py-ta-go ta có:
A B 2 + A C 2 = B C 2 mà AB = AC (gt)
⇒ 2 A B 2 = B C 2 = 2 2 = 4
A B 2 = 2 ⇒ AB= √2(cm) ⇒ AC = √2 (cm)
Tam giác AEC vuông tại E. Theo định lí Py-ta-go ta có:
E A 2 + E C 2 = A C 2 , mà EA = EC (gt)
⇒ 2 E A 2 = A C 2 = 2
E A 2 = 1
⇒ EA = 1(cm) ⇒ EC = 1(cm)
Đúng 0
Bình luận (0)
cho tam giác abc (a<90) phía ngoài tam giác abc vẽ các tam giác abd vuông cân tại d và tam giác ace vuông cân tại e, gọi m là trung điểm của bc chứng minh rằng tam giác dme vuông cân và de <(hoặc bằng) (căng 2)/2(AB+AC)
cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ tam giác ABC vuông cân tại A. Vẽ tam giác ACE vuông cân tại E.C/m rằng BDEC là hình thang cân
Giúp mình với nha!!!!!!!!!!!!!!!!!!!!!
cho tam giác ABC vuông tại A. Vẽ phía ngoài tam giác ABC tam giác ABD vuông cân tại D, vẽ tam giác ACE vuông cân tại E
CM: BDEC là hình thang vuông
Cho tam giác ABC vuông cân tại A có AB = căn 2 cm. Về phía ngoài vẽ tam giác ACD vuông cân tại D
Câu hỏi này thiếu đúng ko bn????
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A, vẽ về phía ngoài tam giác ABC tam giác BCD vuông cân tại B. Gọi N là điểm bất kỳ trên cạnh BD. Trung trực của CN cắt AB tại M. Chứng minh tam giác CMN là tam giác vuông cân.
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?
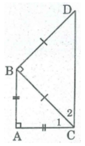
Vì ΔABC vuông cân tại A nên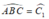 
Lại có: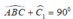 
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên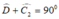 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
Đúng 0
Bình luận (0)
