Cho hình thang ABCD cân , có đáy lớn AB=13; đáy nhỏ DC=5 và AC vuông góc với BD.Tính SABCD

Những câu hỏi liên quan
Cho hình thang cân ABCD có độ dài đáy bé AB bằng 2 cm, độ dài đáy lớn CD gấp ba độ dài đáy AB, độ dài chiều cao AH bằng 4cm. a) Tính độ dài đáy lớn CD của hình thang cân ABCD? b) Tính diện tích hình thang cân ABCD?
Hình thang cân ABCD. Đáy nhỏ CD = 5, đáy lớn AB =13. AC vuông góc BC. Tính Diện tích ABCD ???
Cho hình thang cân ABCD. Biết đáy nhỏ AB = 3cm, cạnh bên BC = 2cm, đáy lớn CD = 5cm. Chu vi hình thang cân ABCD là:
Vì tứ giác ABCD là hình thang cân (gt).
=> AD = BC (Tính chất hình thang cân).
Mà BC = 2 (cm).
=> AD = 2 (cm).
Chu vi hình thang ABCD là:
AB + CD + BC + AD = 3 + 5 + 2 + 2 = 12 (cm).
Đúng 3
Bình luận (0)
p hình thang cân là :
3 + 5 + 2 + 2 = 12 cm
Đ/S : 12 cm
Đúng 1
Bình luận (0)
Bài 1: Cho hình thang cân ABCD có đáy lớn CD = 7cm, góc C = 600, BC = 4cm. Tính độ dài đường trung bình của hình thang.
Bài 2; Cho hình thang cân ABCD có đáy lớn CD = 9cm, AB = 3cm, cạnh BC = 5cm. Tính diện tích hình thang ABCD.
Ghi đầy đủ lời giải giúp mình nhé. Cảm ơn.
Cho hình thang cân ABCD có đáy nhỏ AB1, đáy lớn CD3, cạnh bên
B
C
D
A
2
. Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng: A.
4
3
π
. B.
5
3
π
. C.
2
3
π...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB=1, đáy lớn CD=3, cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng:
A. 4 3 π .
B. 5 3 π .
C. 2 3 π .
D. 7 3 π .
Đáp án D
Ta có: A E = B F = 1
Khi đó: D E = A D 2 − A E 2 = 1
Khi quay hình chữ nhật DEFC quanh trục AB ta được hình trụ có thể tích là:
V 1 = π D E 2 . D C = π .1 2 .3 = 3 π
Khi quay tam giác AED quanh trục AB ta được hình nón có thể tích là:
V 2 = 1 3 π D E 2 . A E = 1 3 π .1 2 .1 = π 3
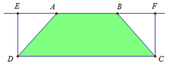
Do đó thể tích vận tròn xoay tạo thành khi cho hình thang quay quanh AB là:
V = V 1 − 2 V 2 = 7 π 3
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có đáy nhỏ
A
B
1
; đáy lớn
C
D
3
, cạnh bên
B
C
D
A
2
. Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng A.
4
3
π
B.
5
3
π
C.
2
3
π...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ A B = 1 ; đáy lớn C D = 3 , cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng
A. 4 3 π
B. 5 3 π
C. 2 3 π
D. 7 3 π
Cho hình thang cân ABCD có đáy nhỏ AB 1 đáy lớn CD 3, cạnh bên
B
C
D
A
2
. Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng A.
5
3
π
B.
4
3...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB =1 đáy lớn CD =3, cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng
A. 5 3 π
B. 4 3 π
C. 7 3 π
D. 2 3 π
Chọn đáp án C
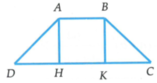
Gọi H, K lần lượt là hình chiếu của A và B trên cạnh CD.
Suy ra ABHK là hình chữ nhật và AB =HK = 1
![]()
Quay hình thang ABCD quanh cạnh AB, ta được một khối tròn xoay có thể tích là V = V 1 - 2 V 2 Trong đó:
+ V1 là thể tích của khối trụ có bán kính đáy r =AH =1 chiều cao h =CD =3
Ta có V = V 1 - 2 V 2 (đvtt).
+ V2 là thể tích của khối nón có bán kính đáy r =AH -1; chiều cao h ' = D H = 1
Ta có V 2 = 1 3 πr 2 h ' = 1 3 π đvtt (đvtt).
Vậy thể tích khối tròn xoay cần tính là V = 3 π - 2 . 1 3 π = 7 3 π (đvtt)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có đáy nhỏ
A
B
1
, đáy lớn
C
D
3
, cạnh bên
B
C
D
A
2
.
Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng: A.
4
3
π
B.
5
3
π
C.
2...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ A B = 1 , đáy lớn C D = 3 , cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng:
A. 4 3 π
B. 5 3 π
C. 2 3 π
D. 7 3 π
Đáp án D
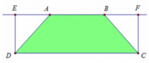
Ta có A E = B F = 1 Khi đó D E = A D 2 − A E 2 = 1
Khi quay hình chữ nhật DEFC quay trục AB ta được hình trụ có thể tích là: V 1 = π . D E 2 . D C = π 1 2 .3 = 3 π
Khi quay tam giác AED quanh trục AB ta được hình nón
có thể tích là V 2 = 1 3 π . D E 2 . A E = 1 3 π .1 2 .1 = π 3 . Do đó thể tích vật tròn xoay tạo thành khi cho hình thang đó quay quanh AB là: V = V 1 − 2 V 2 = 7 π 3 .
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có đáy lớn AB bằng đường chéo AC, đáy nhỏ CD = \(\sqrt{2}BC.\)Tính các góc của hình thang ABCD.













