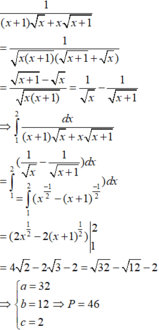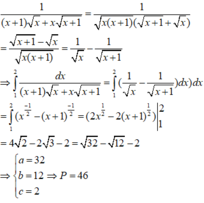Biết a,b,c dương; a + b + c = 1. Chứng minh: \(\frac{a+b^2}{b+c}+\frac{b+c^2}{c+a}+\frac{c+a^2}{a+b}\)\(\ge\)\(2\)

Những câu hỏi liên quan
Tìm các số nguyên dương a,b,c biết \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}=4\)
Tìm ba số dương a,b,c biết a*b=c;b*c=4*a;a*c=9*b.Tìm a,b;c
Theo bài ra. ta có: a x b = c => b = c : a (1) thế vào b x c = 4 x a
Có: c : a x c = 4 x a => c2 = 4 x a2 (2)
a x c = 9 x b => a x c = 9 x c : a => a2 = 9 => a = 3 (a dương)
a = 3 thì (2) <=> c2 = 4 x a2 = 5 x 32 = 36 = 62 => c = 6 (c dương)
Thế vào (1) có: b = c : a = 6 : 3 = 2
Vậy a = 3 ; b = 6 và c = 2
Đúng 0
Bình luận (0)
Biết
∫
1
2
d
x
x
x
+
1
+
x
+
1
x
a
-
b
-
c
, với a, b, c...
Đọc tiếp
Biết ∫ 1 2 d x x x + 1 + x + 1 x = a - b - c , với a, b, c là các số nguyên dương, Tính P = a + b + c.
A. 44
B. 42
C. 46
D. 48
Biết
∫
1
2
d
x
x
+
1
x
+
x
x
+
1
a
−
b
−
c
với a, b, c là các số...
Đọc tiếp
Biết ∫ 1 2 d x x + 1 x + x x + 1 = a − b − c với a, b, c là các số nguyên dương. Tính P = a + b + c .
A. P = 24.
B. P = 12.
C. P = 18.
D. P = 46.
Đáp án D.
Ta có I = ∫ 1 2 d x x x + 1 x + 1 + x
Lại có:
x + 1 + x x + 1 − x = 1 ⇒ I = ∫ 2 2 x + 1 − x x x + 1 d x = ∫ 1 2 1 x − 1 x + 1 d x
= 2 x − 2 x + 1 2 1 = 4 2 − 2 3 − 2 = 32 − 12 − 2 ⇒ a = 32 ; b = 12 ; c = 2
Vậy a + b + c = 46.
Đúng 0
Bình luận (0)
Biết
∫
1
2
d
x
x
+
1
x
+
x
x...
Đọc tiếp
Biết ∫ 1 2 d x x + 1 x + x x + 1 = a − b − c với a, b, c là các số nguyên dương. Tính P = a + b + c
A. P = 24
B. P = 12
C. P = 18
D. P = 46
Biết
∫
1
2
d
x
x
+
1
x
+
x
x
+
1
a
-...
Đọc tiếp
Biết ∫ 1 2 d x x + 1 x + x x + 1 = a - b - c với a,b,c là các số nguyên dương. Tính P = a + b + c
A. P = 24
B. P = 12
C. P = 18
D. P = 46
∫ 1 2 d x x + 1 x + x x + 1 = ∫ 1 2 d x x . x + 1 x + 1 + x = ∫ 1 2 x + 1 - x x . x + 1 x + 1 2 d x = ∫ 1 2 x + 1 - x x + 1 . x d x = ∫ 1 2 d x x - ∫ 1 2 d x x + 1 = 2 x - 2 x + 1 1 2 = 4 2 - 2 3 - 2 - 32 - 12 - 2 ⇒ a = 32 b = 12 c = 2
Đáp án cần chọn là D
Đúng 0
Bình luận (0)
Cho a, b, c thuộc Z. Biết a.b=-c2 và trong ba số a, b, c có 2 số dương, 1 số âm, a<b. Hỏi số nào là số dương, số nào là số âm?
cho các số dương a b c biết a+b+c=1 . Chứng minh √a/1-a + √b/1-b + √c/1-c > 2
Biết
∫
1
2
d
x
(
x
+
1
)
x
+
x
x
+
1
a
-
b
-
c
với a, b...
Đọc tiếp
Biết ∫ 1 2 d x ( x + 1 ) x + x x + 1 = a - b - c với a, b, c là các số nguyên dương. Tính P = a+b+c
A. P = 24
B. P = 12
C. P = 16
D. P = 46
Tìm các số nguyên dương a, b, c biết a³-b³-c³=3abc và a²=2(b+c)
Vì a,b,c dương nên: \(a^3>b^3\Rightarrow a>b\left(1\right)\)
\(a^3>c^3\Rightarrow a>c\left(2\right)\)
Cộng (1) và (2),ta được: 2a>b+c
\(\Rightarrow4a>2\left(b+c\right)\)
\(\Rightarrow4a>a^2\)
\(\Rightarrow4>a\)
Mà a là số chẵn, nên: a=2
Vì a>b>c,nên: 2>b>c ; b=1,c=1
Vậy a,b,c cần tìm lần lượt là 2,1,1
Đúng 0
Bình luận (0)