Cho tứ diện OABCcó O A = a , O B = 2 a ; O C = 3 a đôi vuông góc với nhau tại O. Lấy M là trung điểm của cạnh CA; N nằm trên cạnh CB sao cho C N = 2 3 C B . Tính theo a thể tích khối chóp OAMNB
A. 2 a 3
B. 1 6 a 3
C. 2 3 a 3
D. 1 3 a 3
cho tứ giác abcd cắt ac cắt bd tại o cho diện tích aob=a^2, diện tích cod=b^2 với a,b là 2 số cho trước tìm gtnn của diện tích abcd
Bạn tham khảo ở đây : https://h.vn/hoi-dap/question/198251.html
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB=2a. Thể tích khối tứ diện OO'AB theo a là
A. V = 3 a 3 8
B. V = 3 a 3 4 .
C. V = 3 a 3 6 .
D. V = 3 a 3 12 .
Cho tứ diện OABC có các góc tại đỉnh O đều bằng 90 ° và O A = a , O B = b ; O C = c . Gọi G là trọng tâm của tứ diện. Thể tích của khối tứ diện GABC bằng
A. a b c 6
B. a b c 8
C. a b c 4
D. a b c 24
Chọn D.
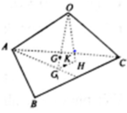
Gọi G1 là trọng tâm của tam giác ABC, H và K lần lượt là hình chiếu của O và G trên mặt phẳng (ABC). Khi đó
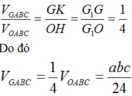
Cho đường tròn $(O ; 2 \mathrm{~cm})$ đường kính $A B$. Lấy điểm $C$ trên đường tròn sao cho $ \widehat{AO C}=45^{\circ}$. Đường thẳng qua $C$ và vuông góc với $A B$ cắt $(O)$ tại $D$. Kéo dài $B C$ và $D A$ cắt nhau tại $M$. Kẻ $M H \perp A B$ tại $H$
a) Chứng minh tứ giác $A H M C$ nội tiếp.
b) Chứng minh $\widehat{A C H}=\widehat{A B C}$
c) Tính diện tích hình quạt $O C B$
Bài làm :
a) Ta có :
\(\widehat{ACB}\text{ là góc nội tếp chắn nửa đường tròn}\)
\(\Rightarrow\widehat{ACB}=90^o\Rightarrow\widehat{ACM}=180^o-\widehat{ACB}=90^o\)
Từ đó ; ta có :
\(\widehat{ACM}+\widehat{AHM}=90+90=180^o\)
=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện = 180 độ
=> Điều phải chứng minh
b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp
\(\Rightarrow\widehat{AMH}=\widehat{ACH}\left(1\right)\)
Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC
\(\Rightarrow\widehat{ADC}=\widehat{ABC}\left(2\right)\)
Vì CD⊥AB ; MH⊥AB
=> CD//MH
=>∠ADC = ∠AMH ( 2góc so le trong ) (3)
Từ (1) ; (2) ; (3)
\(\Rightarrow\widehat{ABC}=\widehat{ACH}\)
=> Điều phải chứng minh
c)∠AOC = 45o
=>∠COB = 180 - 45 = 135o
\(\Rightarrow S_{OCB}=\frac{\pi.R^2.n}{360}=\frac{\pi.2^2.135}{360}=\frac{3}{2}\pi\left(cm^2\right)\)
a) Xét tứ giác AHMC có
góc ACM + góc AHM = 180 độ
Vậy tứ giác AHMC nội tiếp
1. Cho đường tròn (O). Trên đường tròn đó lấy ngẫu nhiên 3 điểm A, B, C. Tính xác suất để \(\Delta ABC\) chứa tâm O của đường tròn.
2. Cho hình cầu tâm (O). Trên mặt hình cầu lấy ngẫu nhiên 4 điểm A, B, C, D. Tính xác suất để hình tứ diện ABCD chứa tâm O của hình cầu.
1. Kẻ đường kính chứa 1 trong 3 điểm A,B,C bất kỳ của (O)
Tam giác ABC chứa tâm O <=>
(*) Có nhiều nhất 2 điểm nằm
trên nửa đường tròn (O) có đường kính như trên , không nhận
cạnh nào là đường kính
(*) ABC là tam giác vuông
Nhận thấy khi tam giác ABC nội tiếp (O) thì A,B,C có 3 trường hợp:
TH1 : 3 điểm cùng nằm trên nửa (O ; DE/2) , không có cạnh nào là đường kính
TH2 : 2 điểm nằm trên nửa (O ; DE/2) ; 1 điểm trên nửa (O) còn lại
TH3 : Tam giác vuông
Biến cố A : " Tam giác ABC chứa tâm O"
=> P(A) = \(\dfrac{2}{3}\)
Cho hình trụ có hai đáy là các hình tròn (O), O ' bán kính bằng a, chiều cao hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O), O ' sao cho . Tính thể tích khối tứ diện A B O O ' theo a
A. a 3 3
B. a 3 5 3
C. 2 a 3 3
D. 2 a 3 5 3
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng a 2 . Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O' sao cho AB' = 2a. Tính thể tích của khối tứ diện OO′B′A.
A. a 3 3 2
B. a 3 2 12
C. a 3 2 6
D. a 3 6
Cho hình trụ có hai đáy là các hình tròn (O), (O’) bán kính bằng a, chiều dài hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O), (O’) sao cho A B = a 6 . Tính thể tích khối tứ diện ABOO’ theo a?
A. a 3 3
B. a 3 5 3
C. 2 a 3 3
D. 2 a 3 5 3
Cho hình trụ có hai đáy là các hình tròn (O), (O’) bán kính bằng a, chiều cao hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O), (O’) sao cho A B = a 6 . Tính thể tích khối tứ diện ABOO’ theo a
![]()
![]()
![]()