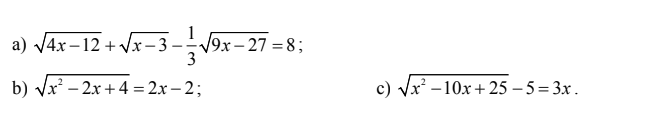
a) \(\sqrt{4x-12}+\sqrt{x-3}-\dfrac{1}{3}\sqrt{9x-27}=8\)(*)

Đk: \(x\ge3\)

(*)\(\Rightarrow2\sqrt{x-3}+\sqrt{x-3}-\sqrt{x-3}=8\)

\(\Leftrightarrow\sqrt{x-3}=4\)

\(\Leftrightarrow x=19\)( nhận)

Vậy S=\(\left\{19\right\}\)

b)\(\sqrt{x^2-2x+4}=2x-2\)    Đk \(x^2-2x+4=\left(x-1\right)^2+3>0\forall x\in R\)

\(\Leftrightarrow x^2-2x+4=4x^2-8x+4\)

\(\Leftrightarrow3x^2-6x=0\)

\(\Leftrightarrow3x\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)

Vậy S=\(\left\{2\right\}\)

c)\(\sqrt{x^2-10x+25}-5=3x\)   ĐK \(x^2-10x+25=\left(x-5\right)^2>0\forall x\in R\)

\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=3x-5\)

\(\Leftrightarrow\left|x-5\right|=3x-5\)

\(\Leftrightarrow\left[{}\begin{matrix}x-5=3x-5\\x-5=5-3x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=\dfrac{10}{4}=\dfrac{5}{2}\left(nhận\right)\end{matrix}\right.\)

Vậy S=\(\left\{\dfrac{5}{2}\right\}\)

Gọi \(x^2=y\) co :

\(2y^2-y-3=0\)

\(\Leftrightarrow2y\left(y+1\right)-3\left(y+1\right)=0\)

\(\Leftrightarrow\left(2y-3\right)\left(y+1\right)=0\\\)

\(\Leftrightarrow\left(2x^2-3\right)\left(x^2+1\right)=0\)

\(\Rightarrow2x^2-3=0\)

còn lại tự làm nha :)))

theo em chắc có thể là như thế này:

xy(6+8+6+3)=2

=>xy23=2

=>xy=2:23

em lm đc đến đây cj có thể lm nốt ko

THẤY J ĐÓ SAI SAI THÌ PHẢI

 kq 2 nha bn ko biet dung ko nua mik moi hc lp 6

@Khôi : Mới học lớp 6 mà làm được sao =))))

Ta có: \(\sqrt{x^2+12}-\sqrt{x^2+5}+5=3x\)

CHú ý: \(\sqrt{x^2+12}-\sqrt{x^2+5}>0\Rightarrow3x>5\Leftrightarrow x>\frac{5}{3}\)

Khi đó Pt <=> \(\left(\sqrt{x^2+5}-3\right)+3\left(x-2\right)-\left(\sqrt{x^2+12}-4\right)=0\)

\(\Leftrightarrow\frac{x^2-4}{\sqrt{x^2+5}+5}+3\left(x-2\right)-\frac{x^2-4}{\sqrt{x^2+12}+4}=0\)

\(\Leftrightarrow\left(x-2\right)\left(\left(x+2\right)\left(\frac{1}{\sqrt{x^2+5}+3}-\frac{1}{\sqrt{x^2+12}+4}\right)+3\right)=0\)

Với \(x>\frac{5}{3}\)ta luôn có: \(\left(x+2\right)\left(\frac{1}{\sqrt{x^2+5}+3}-\frac{1}{\sqrt{x^2+12}+4}\right)+3>0\)

Vậy PT <=> x-2=0

<=> x=2 

Thử lại thấy thỏa mãn

KL: Vậy x=2 là nghiệm duy nhất thỏa mãn

CHÚ Ý: Sau khi tìm ra nghiệm x=2 rồi thì phải thử lại vì ĐK \(x>\frac{5}{3}\) chỉ là ĐK ta tìm được tạm thời để giúp cho bước CM biểu thức trong ngoặc >0 chứ không phải ĐKXĐ chính xác nen phải thử lại, nếu không thử lại đi thi sẽ bị trừ điểm

\(PT\Leftrightarrow\left(m+1\right)x-3x=2m-1\\ \Leftrightarrow x\left(m-2\right)=2m-1\\ \Leftrightarrow x=\dfrac{2m-1}{m-2}\left(m\ne2\right)\)

\(\dfrac{x-1}{13}-\dfrac{2x-13}{15}=\dfrac{3x-15}{27}-\dfrac{2x-27}{29}\)

\(\Leftrightarrow\dfrac{x-1}{13}-1-\dfrac{2x-13}{15}-1=\dfrac{3x-15}{27}-1-\dfrac{2x-27}{29}-1\)

\(\Leftrightarrow\dfrac{x-1-13}{13}-\dfrac{2x-13-15}{15}=\dfrac{3x-15-27}{27}-\dfrac{4x-27-29}{29}\)

\(\Leftrightarrow\dfrac{x-14}{13}-\dfrac{2x-24}{15}=\dfrac{3x-42}{27}-\dfrac{4x-56}{29}\)

\(\Leftrightarrow\dfrac{x-14}{13}-\dfrac{2\left(x-14\right)}{15}-\dfrac{3\left(x-14\right)}{27}-\dfrac{4\left(x-14\right)}{29}=0\)

\(\Leftrightarrow\left(x-14\right)\left(\dfrac{1}{13}-\dfrac{2}{15}-\dfrac{3}{27}-\dfrac{4}{29}\right)=0\)

\(\Leftrightarrow x-14=0\) ( Vì: \(\dfrac{1}{13}-\dfrac{2}{15}-\dfrac{3}{27}-\dfrac{4}{29}\ne0\))

\(\Leftrightarrow x=14\)

\(x^2-3x+1=\dfrac{5\sqrt{3}}{3}\sqrt{x^4+x^2+1}\)

\(\Leftrightarrow\)\(\left(x^2-3x+1\right)^2=\dfrac{25}{3}\left(x^4+x^2+1\right)\)

\(\Leftrightarrow\)\(x^4-6x^3+11x^2-6x+1=\dfrac{25}{3}x^4+\dfrac{25}{3}x^2+\dfrac{25}{3}\)

\(\Leftrightarrow11x^4+9x^3-4x^2+9x+11=0\)

\(\Leftrightarrow\left(x+1\right)\left(11x^3-2x^2-2x+11\right)=0\)

\(\Rightarrow x=-1\)