Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và \(SA\perp mp\left(ABCD\right)\). Trong mp(SAB) hạ \(AM\perp SB\)\(\left(M\in SB\right)\). Tính góc tạo bởi mp(SDM) và mp(ABCD) .
\(\widehat{MAB}\).\(180^o-\widehat{MAB}\).\(\widehat{BMA}\).\(180^o-\widehat{BMA}\).Hướng dẫn giải: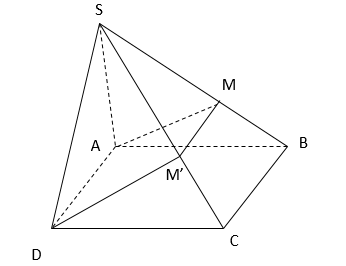
Có \(SA\perp mp\left(ABCD\right)\) nên \(mp\left(SAB\right)\perp mp\left(ABCD\right)\).
Ta chứng minh được \(BC\perp mp\left(SAB\right)\) vì vậy \(mp\left(SAB\right)\perp mp\left(SBC\right)\).
Do \(AM\perp SB\Rightarrow AM\perp mp\left(SBC\right)\). Vì vậy \(M'M\perp AM\), mà \(SA\perp AD\Rightarrow SA\perp M'M\).
Suy ra \(M'M\perp mp\left(SAB\right)\) hay \(mp\left(ADM'M\right)\perp mp\left(SAB\right)\).
Suy ra góc tạo bởi hai mp(ADMM') và mp(ABCD) là \(\left(AM,AB\right)\).
Trong mp(SAB) có tam giác SAB là tam giác vuông và \(AM\perp SB\) nên \(\left(AM,AB\right)< 90^o\Leftrightarrow\widehat{AMB}=\left(AM,AB\right)\).

