Cho hình chóp tứ giác \(S.ABCD\) có đáy ABCD là hình vuông cạnh \(a\), \(SA=SB=a\), \(SD=\sqrt{2}a\). Góc giữa \(\left(SAB\right)\) và \(\left(SBD\right)\) bằng \(\alpha\). Chọn khẳng định đúng trong các khẳng định sau.
\(cos\alpha=\dfrac{1}{3}\).\(cos\alpha=-\dfrac{2}{5}\).\(cos\alpha=\dfrac{1}{2}\).\(cos\alpha=\dfrac{2}{3}\).Hướng dẫn giải: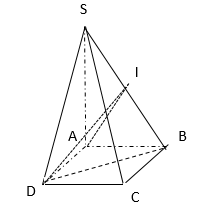
Gọi I là trung điểm của SB ta có \(DI\perp AB\) (vì tam giác SBD đều) và \(AI\perp AB\) (vì tam giác SAB) đều. Vậy góc giữa hai mặt phẳng (SAB) và (SBD) bằng góc \(\left(IA,ID\right)\).
Ta có: \(AD=\sqrt{2}a\) (đường chéo hình vuông) và AI = DI = \(\dfrac{a\sqrt{3}}{2}\) (đường cao tam giác đều).
Áp dụng định lý cosin cho góc I trong tam giác AID ta có:
\(cos\widehat{AID}=\dfrac{AI^2+ID^2-AD^2}{2AI.DI}=\)\(\dfrac{\left(\dfrac{a\sqrt{3}}{2}\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2-\left(a\sqrt{2}\right)^2}{2.\left(\dfrac{a\sqrt{3}}{2}\right).\left(\dfrac{a\sqrt{3}}{2}\right)}=-\dfrac{1}{3}\).
Vậy \(cos\left(IA,ID\right)=\dfrac{1}{3}\).

