Em có thể quan sát vào hình ảnh:

Lực Coriolit là lực làm lệch hướng chuyển động của các vật thể chuyển động trên Trái Đất, Ở BCB vật chuyển động bị lệch về bên phải, ở BCN bị lệch về bên trái theo hướng chuyển động ban đầu
- Ở Bán cầu bắc: Gió Mậu dịch và đông cực dưới tác động của lực Côriolit bị lệch về bên phải trở thành hướng ĐB - TN
- Ở Bán cầu Nam: Gió Mậu dịch và đông cực dưới tác động của lực Côriolit bị lệch về bên trái trở thành hướng ĐN - TB
Chúc em học tốt!
Tham khảo :
1. Phân tích tác động của lực Coriolit đến hoàn lưu khí quyển trên trái đất.
Trả lời:
– Không khí trên mặt đất ở Xích đạo bị đốt nóng, nở ra và bay lên cao, đến một độ cao nào đó thì bị lạnh đi. Do ở phía dưới vẫn có các dòng khí đi lên, nên khí lạnh này không hạ xuống được mà phải đi về phía hai cực và bị lệch về phía đông do tác dụng của lực Coriolis. Tới khoảng vĩ độ 30° – 35°, độ lệch đã lên đến 90( so với kinh tuyến, các dòng khí chuyển động song song với vĩ tuyến. Tại đây, không khí đã lạnh hẳn, hạ xuống rất nhanh, tạo ra các vùng áp cao ở bên dưới và hình thành nên đai áp cao cận nhiệt đới. Với sự xuất hiện của đai áp cao này làm phát sinh các đai hoang mạc cận nhiệt trên các lục địa và vùng lặng gió trên các đại dương.
– Do sự chênh lệch về khí áp nên có gió thổi từ hai khu áp cao cận nhiệt đới về phía Xích đạo và phía hai cực.
+ Các luồng gió thổi về phía Xích đạo dọc theo chiều kinh tuyến nhưng dưới tác động của lực Coriolis các luồng gió này bị lệch hướng và thổi theo hướng đông bắc – tây nam ở bán cầu Bắc và đông nam – tây bắc ở bán cầu Nam. Gió này gọi là gió Mậu dịch (Tín phong).
+ Các luồng gió thổi từ các khu áp cao cận nhiệt về phía cực bị lực Coriolis làm lệch về phía đông, đến khoảng vĩ độ 45° – 50° hầu như thổi theo hướng tây
– đông, tạo thành đai gió Tây (gió Tây ôn đới).
+ Các luồng gió thổi từ áp cao cực về phía Xích đạo cũng chịu sự tác động của lực Coriolis, đến các vĩ độ 65° đã có phương song song với vĩ tuyến và thổi theo hướng từ đông và tây, nên được gọi là gió Đông (gió Đông cực).
+ Vùng ôn đới nằm giữa đai gió Đông và đai gió Tây là vòng đai lặng gió. ở đây, gió thổi đến từ hai phía Bắc và Nam ngược hướng nhau là nguyên nhân động lực để hình thành đai áp thấp ôn đới.
2. Phân tích tác động của lực Coriolit đến dòng biển, dòng chảy, sông ngòi.
Trả lời:
* Tác động của lực Coriolis đến các dòng biển
– Những dòng biển chảy từ Xích đạo về phía bắc (hải lưu Gơn strim hay còn gọi là “d0fng vịnh”, Bắc Đại Tây Dương, Cư-rô-si-vô, Bắc Thái Bình Dương) đều bị lệch sang phía Đông và chảy theo hướng tây nam – đông hắc.
– Những dòng biển chảy từ Xích đạo về phía nam (dương lưu tín phong Nam Đại Tây Dương chảy ven bờ đông Bra-xin, Ma-đa-ga-xca, Đông úc,…) càng chảy về phía nam càng lệch về phía đông, đến vĩ tuyến 40 – 50° Nam thì lệch
hẳn về phía đông
– Các dòng biển chảy từ phía đông sang phía tây dọc Xích đạo ở các đại dương, càng về phía tây càng tỏa rộng ra. Phần trên Xích đạo, các nhánh bị lệch về phải chảy lên phía bắc. Phần dưới Xích đạo, lệch về trái và chảy về phía nam.
* Tác động của lực Coriolis đến các dòng chảy của sông: Trong mỗi con sông ở bán cầu Bắc, áp lực của dòng chảy lên bờ phải của sông mạnh hơn so với bờ trái, còn ở bán cầu Nam thì ngược lại.
Trên Bắc bán cầu thì đây là những luồng gió thổi chủ yếu theo hướng (chiều) đông bắc-tây nam, còn trên Nam bán cầulà hướng (chiều) đông nam-tây bắc (do ảnh hưởng của lực Coriolis).
Cả hai loại gió đều thổi từ nơi có vận tốc dài nhỏ về nơi có vận tốc dài lớn hơn ( từ vĩ độ thấp về vĩ độ cao )nếu không có lực coliolis thì hướng gió là như nhau .Do độ lớn của lực coliolis khác nhau nên hướng gió của hai loại gió này khác nhau
Ở khu vực XĐ , lực coliolis nhỏ nên hướng gió tín phong ở BBC chuyển từ hướng B thành ĐB , ở NBC chuyển từ hướng N thành ĐN.
Khu vực cực lực coliolis rất mạnh nên hướng gió đông cực đều chuyển thành hướng đông thổi gần như song song với vĩ tuyến
Bạn tham khảo:
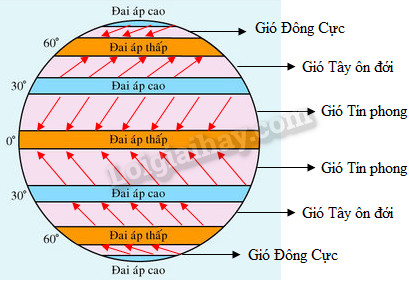
– Do sự chênh lệch về khí áp nên có gió thổi từ hai khu áp cao cận nhiệt đới về phía Xích đạo và phía hai cực. + Các luồng gió thổi về phía Xích đạo dọc theo chiều kinh tuyến nhưng dưới tác động + Các luồng gió thổi từ các khu áp cao cận nhiệt về phía cực bị lực Coriolis làm lệch về phía đông, đến khoảng vĩ độ 45° – 50° hầu như thổi theo hướng tây – đông, tạo thành đai gió Tây (gió Tây ôn đới). + Các luồng gió thổi từ áp cao cực về phía Xích đạo cũng chịu sự tác động của lực Coriolis, đến các vĩ độ 65° đã có phương song song với vĩ tuyến và thổi theo hướng từ đông và tây, nên được gọi là gió Đông (gió Đông cực). + Vùng ôn đới nằm giữa đai gió Đông và đai gió Tây là vòng đai lặng gió. ở đây, gió thổi đến từ hai phía Bắc và Nam ngược hướng nhau là nguyên nhân động lực để hình thành đai áp thấp ôn đới
















