Chọn C
Để cho gọn ta chọn a=2
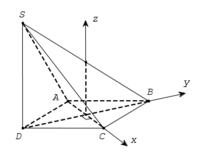
Chọn hệ trục tọa độ Oxyz như hình vẽ với O(0;0;0) và C(1;0;0), B(0; 3 ;0) S(0; - 3 ; x) với x =SD>0
Suy ra A(-1;0;0) và D(0;- 3 ;0)
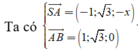
VTPT của mặt phẳng (SAB) là
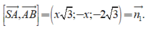
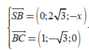
VTPT của mặt phẳng (SBC) là
![]()
Từ giả thiết bài toán, ta có
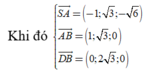
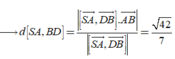
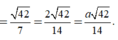
Chọn C
Để cho gọn ta chọn a=2

Chọn hệ trục tọa độ Oxyz như hình vẽ với O(0;0;0) và C(1;0;0), B(0; 3 ;0) S(0; - 3 ; x) với x =SD>0
Suy ra A(-1;0;0) và D(0;- 3 ;0)
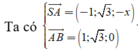
VTPT của mặt phẳng (SAB) là
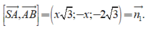
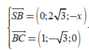
VTPT của mặt phẳng (SBC) là
![]()
Từ giả thiết bài toán, ta có
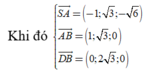
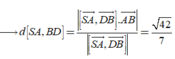
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB =a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 o (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và SC bằng
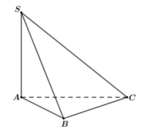
A. a
B. a 2 2
C. a 3 2
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA=a và vuông góc với mặt đáy (ABCD). Khoảng cách giữa hai đường thẳng SC và BD bằng
A. a 3 4
B. a 6 3
C. a 2
D. a 6 6
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a và A B C ^ = 60 ° . Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 30 ° . Tính khoảng cách giữa hai đường thẳng SA, CD theo a ?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy. Khoảng cách giữa hai đường thẳng SD,BC bằng
![]()
![]()
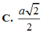
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=a 3 Cạnh bên SA =a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng
A. 3 2
B. 14 4
C. 3 5
D. 22 5
Hình chóp S.ABCD có đáy là hình thoi cạnh a, góc B A C ^ = 60 0 SA vuông góc với mp(ABCD) góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60 0 Khoảng cách từ A đến mp (SBC) bằng
A. a 2 3
B. 2a
C. 3 a 4
D. a
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên SA = SB = SC = SD = a√2. Gọi I và K lần lượt là trung điểm của AD và BC.
a) Chứng minh mặt phẳng (SIK) vuông góc với mặt phẳng (SBC).
b) Tính khoảng cách giữa hai đường thẳng AD và SB.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Biết SA = a AB = 2a RC = a * sqrt(3) a) Chứng minh CD. (SAD) SD và (ABCD). c) Tính khoảng cách từ điểm D đến (SBC). b) Tính góc giữa
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD).
a) Chứng minh BD ⊥ SC.
b) Chứng minh (SAB) ⊥ (SBC).
c) Cho SA = (a√6)/3. Tính góc giữa SC và mặt phẳng (ABCD).