Đáp án cần chọn là: C
dùng dung dịch quỳ tím ta chia thành 3 nhóm
- Nhóm (I): quỳ tím hóa đỏ : NH4Cl, H2SO4
- Nhóm (II) quỳ tím hóa xanh: NaOH, Ba(OH)2
- Nhóm (III): quỳ tím không đổi màu: NaCl, Na2SO4
- Cho lần lượt từng chất ở nhóm (II) vào từng chất ở nhóm (I)
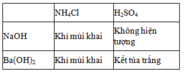
- Cho Ba(OH)2 nhận biết được vào từng chất ở nhóm (III), chất tạo kết tủa trắng là Na2SO4, chất không hiện tượng là NaCl



