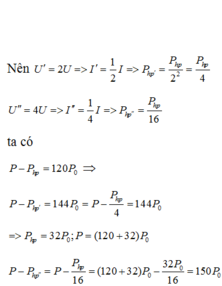Điện năng từ một trạm phát điện được đưa đến một khu tái định cư bằng đường dây truyền tải một pha. Cho biết, nếu điện áp tại đầu truyền đi tăng từ U lên 2U thì số hộ dân được trạm cung cấp đủ điện năng từ 120 lên 144. Cho rằng chỉ tính đến hao phí trên đường dây, công suất tiêu thụ điện của các hộ dân đều như nhau, công suất của trạm phát không đổi và hệ số công suất trong các trường hợp đều bằng nhau. Nếu điện áp truyền đi là 4 U thì trạm phát huy này cung cấp đủ điện năng cho
A. 168 hộ dân
B. 504 hộ dân
C. 192 hộ dân
D. 150 hộ dân
Đáp án D
Gọi công suất phát là P, công suất mỗi hộ gia đình là P0 ; công suất hao phí trong 3 trường hợp là Php ; Php’ và Php’’.
Ta biết rằng : ![]()
Khi U tăng bao nhiêu lần thì I giảm bấy nhiêu lần (theo công thức máy biến áp)