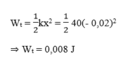Các câu hỏi tương tự
Một con lắc lò xo nằm ngang dao động điều hoà. Lò xo có độ cứng k = 40 N/m. Khi quả cầu con lắc qua vị trí có li độ x = -2 cm thì thế năng của con lắc bằng
A. -0,016 J. B. 0,008 J.
C. -0,08 J. D. 0,016 J.
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng k = 100 N/m. Khi vật có khối lượng m của con lắc đi qua vị trí có li độ x = 4 cm theo chiều âm thì thế năng của con lắc đó là bao nhiêu ?
A. 8 J B. 0,08 J C. - 0,08 J D. Không xác định được vì chưa biết giá trị của khối lượng m
Một con lắc lò xo dao động điều hòa. Lò xo có độ cứng k = 80 N/m. Khi vật m của con lắc đang qua vị trí có li độ cm thì thế năng con lắc là bao nhiêu ?
A. – 0,008J.
B. 0,016J.
C. – 0,016J.
D. 0,008J.
Một con lắc lò xo dao động điều hòa. Lò xo có độ cứng k = 40 N/m. Khi quả cầu con lắc qua vị trí có li độ x = – 2 cm thì thế năng của con lắc là
A. -0,016 J
B. 0,008 J
C. -0,80 J
D. 0,016 J
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng k 100 N/m. Khi vật có khối lượng m của con lắc đi qua vị trí có li độ x 4 cm theo chiều âm thì thế năng của con lắc đó là bao nhiêu? A. 8 J. B. 0,08 J. C. –0,08 J. D. –8 J.
Đọc tiếp
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng k = 100 N/m. Khi vật có khối lượng m của con lắc đi qua vị trí có li độ x = 4 cm theo chiều âm thì thế năng của con lắc đó là bao nhiêu?
A. 8 J.
B. 0,08 J.
C. –0,08 J.
D. –8 J.
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng k 100 N/m. Khi vật có khối lượng m của con lắc đi qua vị trí có li độ x 4 cm theo chiều âm thì thế năng của con lắc đó là bao nhiêu? A. 8 J B. 0,08 J C. –0,08 J D. –8 J
Đọc tiếp
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng k = 100 N/m. Khi vật có khối lượng m của con lắc đi qua vị trí có li độ x = 4 cm theo chiều âm thì thế năng của con lắc đó là bao nhiêu?
A. 8 J
B. 0,08 J
C. –0,08 J
D. –8 J
Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng k = 100 N/m. Khi vật có khối lượng m của con lắc đi qua vị trí có li độ x = 4 cm theo chiều âm thì thế năng của con lắc đó là bao nhiêu?
A. 8 J
B. 0,08 J
C. –0,08 J
D. –8 J
Một con lắc lò xo mà lò xo nhẹ có độ cứng 100 N/m và vật nhỏ dao động điều hòa. Khi vật có động năng 0,01 J thì nó cách vị trí cân bằng 1 cm. Hỏi khi nó có động năng 0,005 J thì nó cách vị trí cân bằng bao nhiêu? A. 6 cm B. 4,5 cm C.
2
cm D. 3 cm
Đọc tiếp
Một con lắc lò xo mà lò xo nhẹ có độ cứng 100 N/m và vật nhỏ dao động điều hòa. Khi vật có động năng 0,01 J thì nó cách vị trí cân bằng 1 cm. Hỏi khi nó có động năng 0,005 J thì nó cách vị trí cân bằng bao nhiêu?
A. 6 cm
B. 4,5 cm
C. 2 cm
D. 3 cm
Một con lắc lò xo dao động điều hòa, lò xo có độ cứng k = 40 N/m. Với mốc thế năng tại ví trí cân bằng thì khi vật có li độ là x = _2 (cm) thế năng của con lắc là
A. 0,016 J.
B. 80 J.
C. 0,008 J.
D. –0,016 J.