Có tất cả 6 hình thang, đó là:
ABCD, CDFE, EFHG, ABFE, CDHG, ABHG
Có tất cả 6 hình thang, đó là:
ABCD, CDFE, EFHG, ABFE, CDHG, ABHG
Trên hình vẽ dưới có bao nhiêu hình thang
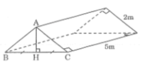
Hình vẽ là chiếc lều ở một trại hè với các kích thước trên hình ABC là tam giác vuông cân. Số vải bạt cần có để dựng lều đó là bao nhiêu?
Cho tam giác ABC, gọi M, N và P lần lượt là trung điểm của AB, AC và BC. Hỏi có bao nhiêu hình thang trong hình vẽ ?
A. 7
B. 6
C. 8
D. 9
Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
a) Hình thang có hai góc vuông là hình chữ nhật.
b) Hình thang cân có một góc vuông là hình chữ nhật.
c) Hình bình hành có một góc vuông là hình chữ nhật.
d) Hình bình hành có hai đường chéo cắt nhau trại trung điểm mỗi đường là hình chữ nhật.
Cho hình thang can ABCD M và N là trung điểm của hai đáy I và K là trung điểm của hai cạnh bên vẽ hình đối xứng của hình thang cân trên qua 2 đường thẳng MN và IK
Vẽ hình và giải bài tập
Cho tam giác ABC cân tại A, đường cao AD. Gọi E là điểm đối xứng với D qua trung điểm M của AC.
a) Chứng minh: Tứ giác AECD là hình chữ nhật.
b) Chứng minh: Tứ giác ABDM là hình thang.
c) Để hình thang ABDM là hình thang cân thì tam giác ABC là tam giác gì?
d) Để hình chữ nhật AECD là hình vuông thì tam giác ABC cân có điều kiện gì?Vẽ hình và giải bài tập
ΔABC cân tại A có góc A = 54 độ . Các đường trung tuyến BE,CF
a, Tứ giác BCEF có phải hình thang ko ? Tính các góc
b, C/m tứ giác BCEF là hình thang cân
Có vẽ hình
3. Cho hình thang ABCD AB//CD. Hai đường chéo AC và BD vuông góc với nhau. Vẽ đường cao BH và vẽ hình bình hành ABEC. Biết BD=12; DH=7,2; Tính:
a) Độ dài đoạn thẳng DE
b) Tính diện tích hình thang ABCD