Bài 6: Phép trừ các phân thức đại số

\(\dfrac{5x+y^2}{x^2y}-\dfrac{5y+x^2}{xy^2}\)

\(=\dfrac{y\left(5x+y^2\right)}{x^2y^2}-\dfrac{x\left(5y-x^2\right)}{x^2y^2}\)

\(=\dfrac{5xy+y^3}{x^2y^2}-\dfrac{5xy+x^3}{x^2y^2}\)

\(=\dfrac{5xy+y^3-5xy+x^3}{x^2y^2}\)

\(=\dfrac{\left(5xy-5xy\right)+x^3+y^3}{x^2y^2}\)

\(=\dfrac{x^3+y^3}{x^2y^2}\)

\(\dfrac{5x+y^2}{x^2y}-\dfrac{5y-x^2}{xy^2}=\dfrac{y\left(5x+y^2\right)}{y\cdot x^2y}-\dfrac{x\left(5y-x^2\right)}{x\cdot xy^2}\)

\(=\dfrac{5xy+y^3-5xy+x^3}{x^2y^2}=\dfrac{x^3+y^3}{x^2y^2}\) \(\left(x,y\ne0\right)\)

\(\dfrac{5x-5}{\left(x+1\right)^2}:\dfrac{20x^2-20}{3x+3}\\ =\dfrac{5\left(x-1\right)}{\left(x+1\right)^2}:\dfrac{20\left(x^2-1\right)}{3\left(x+1\right)}\\ =\dfrac{5\left(x-1\right)}{\left(x+1\right)^2}\cdot\dfrac{3\left(x+1\right)}{20\left(x^2-1\right)}\\ =\dfrac{3}{4\left(x+1\right)^2}\)

\(\dfrac{5x-5}{\left(x+1\right)^2}-\dfrac{20x^2-20x}{3x+3}\\ =\dfrac{5\left(x-1\right)}{\left(x+1\right)^2}-\dfrac{20x\left(x-1\right)}{3\left(x+1\right)}\\ =\dfrac{15\left(x-1\right)}{3\left(x+1\right)^2}-\dfrac{20x\left(x^2-1\right)}{3\left(x+1\right)^2}\\ =\dfrac{15x-15-20x^3+20x}{3\left(x+1\right)^2}\\ =\dfrac{-20x^3+35x-15}{3\left(x+1\right)^2}\)

cần gấp ạaa!!

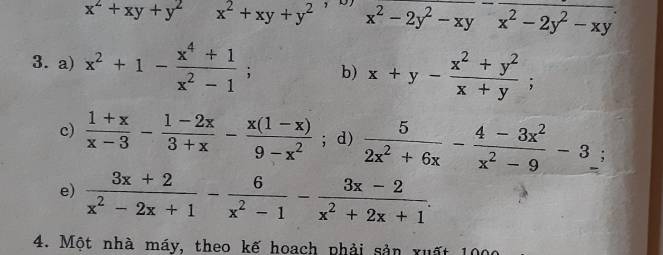
a: \(=\dfrac{\left(x^2+1\right)\left(x^2-1\right)-x^4-1}{x^2-1}\)

\(=\dfrac{x^4-1-x^4-1}{x^2-1}=-\dfrac{2}{x^2-1}\)

b: \(=\dfrac{\left(x+y\right)^2-x^2-y^2}{x+y}\)

\(=\dfrac{x^2+2xy+y^2-x^2-y^2}{x+y}=\dfrac{2xy}{x+y}\)

c: \(=\dfrac{\left(x+1\right)\left(x+3\right)+\left(2x-1\right)\left(x-3\right)+x\left(1-x\right)}{x^2-9}\)

\(=\dfrac{x^2+4x+3+2x^2-7x+3+x-x^2}{x^2-9}\)

\(=\dfrac{2x^2-2x+6}{x^2-9}\)

d: \(\dfrac{5}{2x^2+6x}-\dfrac{4-3x^2}{x^2-9}-3\)

\(=\dfrac{5}{2x\left(x+3\right)}+\dfrac{3x^2-4}{\left(x-3\right)\left(x+3\right)}-3\)

\(=\dfrac{5\left(x-3\right)+2x\left(3x^2-4\right)-3\cdot2x\left(x^2-9\right)}{2x\left(x+3\right)\left(x-3\right)}\)

\(=\dfrac{5x-15+6x^3-8x-6x^3+54x}{2x\left(x+3\right)\left(x-3\right)}\)

\(=\dfrac{51x-15}{2x\left(x+3\right)\left(x-3\right)}\)

e: \(=\dfrac{3x+2}{\left(x-1\right)^2}-\dfrac{6}{\left(x-1\right)\left(x+1\right)}-\dfrac{3x-2}{\left(x+1\right)^2}\)

\(=\dfrac{\left(3x+2\right)\left(x+1\right)^2-6\left(x^2-1\right)-\left(3x-2\right)\left(x-1\right)^2}{\left(x-1\right)^2\cdot\left(x+1\right)^2}\)

\(=\dfrac{\left(3x+2\right)\left(x+1\right)\left(x+1\right)-\left(3x-2\right)\left(x-1\right)\left(x-1\right)-6\left(x^2-1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)^2}\)

\(=\dfrac{\left(3x^2+5x+2\right)\left(x+1\right)-\left(3x^2-5x+2\right)\left(x-1\right)-6\left(x^2-1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)^2}\)

\(=\dfrac{3x^3+8x^2+7x+2-3x^3+8x^2-7x+2-6x^2+6}{\left(x-1\right)^2\left(x+1\right)^2}\)

\(=\dfrac{10x^2+10}{\left(x-1\right)^2\left(x+1\right)^2}\)

=>\(\left(\dfrac{x+1}{2021}+1\right)+\left(\dfrac{x+2}{2020}+1\right)+\left(\dfrac{x+3}{2019}+1\right)+\left(\dfrac{x+2028}{2}-3\right)=0\)

=>x+2022=0

=>x=-2022

Câu 4:

Gọi số học sinh nam, số học sinh nữ lần lượt là a,b

Theo đề,ta có: a+b=45 và 120000a+100000b=4900000

=>a=20 và b=25

Cau 3:

Gọi thể tích dầu ban đầu ở thùng A và thùng B lần lượt là a,b

Theo đề, ta có:

a=4b và a-40=b+20

=>a-4b=0 và a-b=60

=>a=80 và b=20

Câu 1: 

Hiệu số phần bằng nhau:

3-1=2(phần)

Tuổi mẹ hiện nay:

28:2 x 3= 42(tuổi)

Tuổi An hiện nay:

42:3=14(tuổi)

Câu 2: TH1: 5 kí táo và 7 kí xoài

TH2: 10 kí táo và 4 kí xoài

TH3: 15 kí táo và 1 kí xoài

-2x thì làm sao bằng 2x được bạn, trừ khi x=0

\(đk:x\ne7;-7\\ =\dfrac{x+7}{x-7}-\dfrac{x-7}{x+7}+\dfrac{4x^2}{\left(x-7\right)\left(x+7\right)}\\ =\dfrac{\left(x+7\right)^2-\left(x-7\right)^2+4x^2}{\left(x-7\right)\left(x+7\right)}\\ =\dfrac{x^2+14x+49-x^2+14x-49+4x^2}{\left(x-7\right)\left(x+7\right)}\\ =\dfrac{4x^2+28x}{\left(x-7\right)\left(x+7\right)}\\ =\dfrac{4x\left(x+7\right)}{\left(x-7\right)\left(x+7\right)}\\ =\dfrac{4x}{x-7}\)

\(\dfrac{x+7}{x-7}-\dfrac{x-7}{x+7}+\dfrac{4x^2}{x^2-49}\left(x\ne\pm7\right)\)

\(=\dfrac{\left(x+7\right)^2}{x^2-49}-\dfrac{\left(x-7\right)^2}{x^2-49}+\dfrac{4x^2}{x^2-49}\)

\(=\dfrac{x^2+14x+49-x^2+14x-49+4x^2}{x^2-49}\)

\(=\dfrac{4x^2+28x}{x^2-49}=\dfrac{4x\left(x+7\right)}{\left(x+7\right)\left(x-7\right)}=\dfrac{4x}{x-7}\)

\(\dfrac{x+7}{x-7}-\dfrac{x-7}{x+7}+\dfrac{4x^2}{x^2-49}\\ =\dfrac{x+7}{x-7}-\dfrac{x-7}{x+7}+\dfrac{4x^2}{\left(x-7\right)\left(x+7\right)}\)

\(=\dfrac{\left(x+7\right)^2}{\left(x-7\right)\left(x+7\right)}-\dfrac{\left(x-7\right)^2}{\left(x-7\right)\left(x+7\right)}+\dfrac{4x^2}{\left(x-7\right)\left(x+7\right)}\)

\(=\dfrac{x^2+14x+49-x^2+14x-49+4x^2}{\left(x-7\right)\left(x+7\right)}\)

\(=\dfrac{x^2-x^2+4x^2+14x+14x+49-49}{\left(x-7\right)\left(x+7\right)}\)

\(=\dfrac{4x^2+28x}{\left(x-7\right)\left(x+7\right)}\)

\(=\dfrac{4x\left(x+7\right)}{\left(x-7\right)\left(x+7\right)}\\ =\dfrac{4x}{x-7}\)

\(đk:x\ne2\\ =\dfrac{x^2-8}{4x-8}-\dfrac{x-3}{x-2}\\ =\dfrac{x^2-8}{4\left(x-2\right)}-\dfrac{x-3}{x-2}\\ =\dfrac{x^2-8-4\left(x-3\right)}{4\left(x-2\right)}\\ =\dfrac{x^2-8-4x+12}{4\left(x-2\right)}\\ =\dfrac{x^2-4x+4}{4\left(x-2\right)}\\ =\dfrac{\left(x-2\right)^2}{4\left(x-2\right)}\\ =\dfrac{x-2}{4}\)