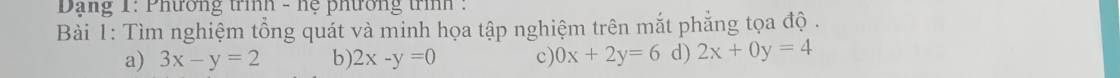a: Xét tứ giác OIBE có \(\widehat{OIE}=\widehat{OBE}=90^0\)
nên OIBE là tứ giác nội tiếp
Xét tứ giác OIFC có \(\widehat{OIF}+\widehat{OCF}=90^0+90^0=180^0\)
nên OIFC là tứ giác nội tiếp
b: Ta có: \(\widehat{OFI}=\widehat{OCI}\)(OIFC nội tiếp)
\(\widehat{OEI}=\widehat{OBI}\)(OEBI nội tiếp)
mà \(\widehat{OCI}=\widehat{OBI}\)(ΔOBC cân tại O)
nên \(\widehat{OFI}=\widehat{OEI}\)
=>ΔOEF cân tại O
Ta có: ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
c: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
Xét (O) có
MB,MK là các tiếp tuyến
Do đó: MB=MK
Xét (O) có
NK,NC là các tiếp tuyến
Do đó: NK=NC
Chu vi tam giác AMN là:
AM+MN+NA
=AM+MK+NK+NA
=AM+MB+AN+NC
=AC+AC
\(=2R\sqrt{3}\)
Đúng 0
Bình luận (0)
a: Khi m=1 thì (d): \(y=2x-1^2+9=2x+8\)
Phương trình hoành độ giao điểm là:
\(x^2=2x+8\)
=>\(x^2-2x-8=0\)
=>(x-4)(x+2)=0
=>\(\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
Khi x=4 thì \(y=2\cdot4+8=16\)
Khi x=-2 thì \(y=2\cdot\left(-2\right)+8=4\)
vậy: (d) cắt (P) tại A(4;16); B(-2;4)
b: Phương trình hoành độ giao điểm là:
\(x^2=2x-m^2+9\)
=>\(x^2-2x+m^2-9=0\)
Để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung thì \(1\cdot\left(m^2-9\right)< 0\)
=>\(m^2-9< 0\)
=>\(m^2< 9\)
=>-3<m<3
Đúng 1
Bình luận (0)
a: 3x-y=2
=>y=3x-2
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=3x-2\end{matrix}\right.\)
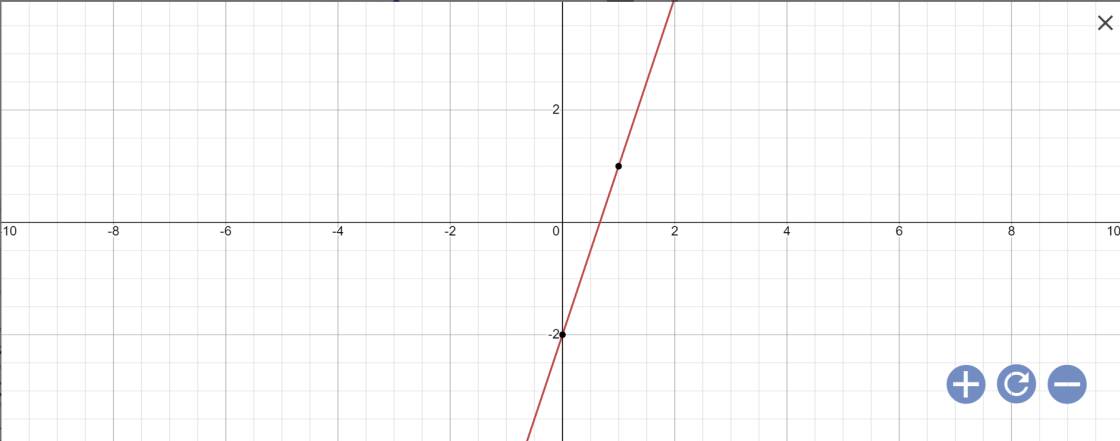
b: 2x-y=0
=>y=2x
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=2x\end{matrix}\right.\)
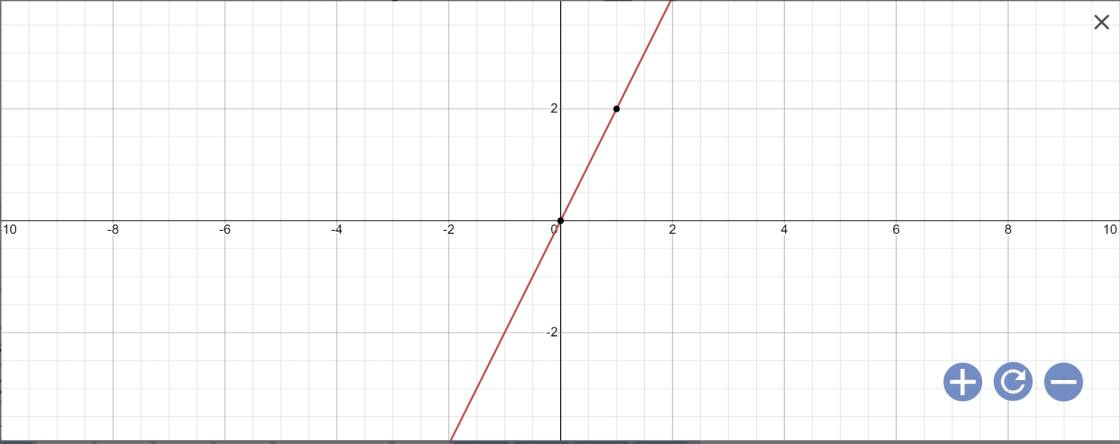
c: 0x+2y=6
=>2y=6
=>y=3
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=3\end{matrix}\right.\)
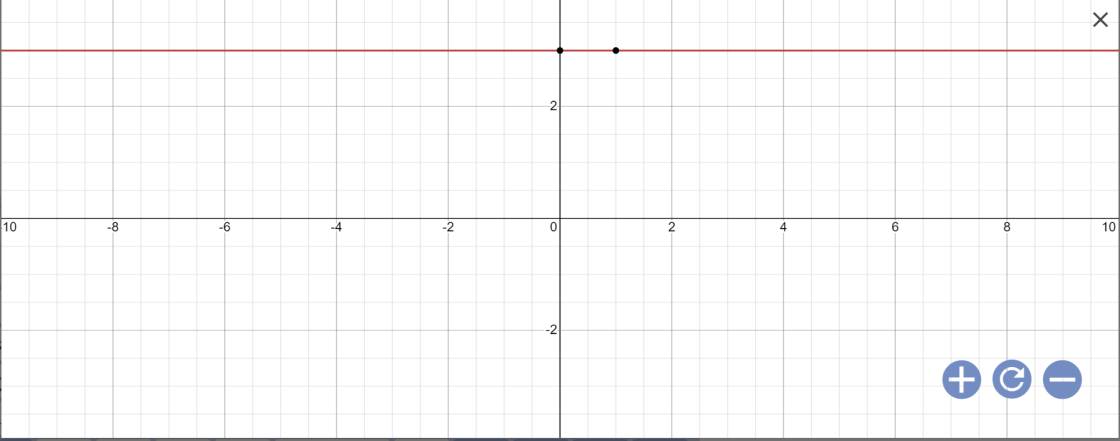
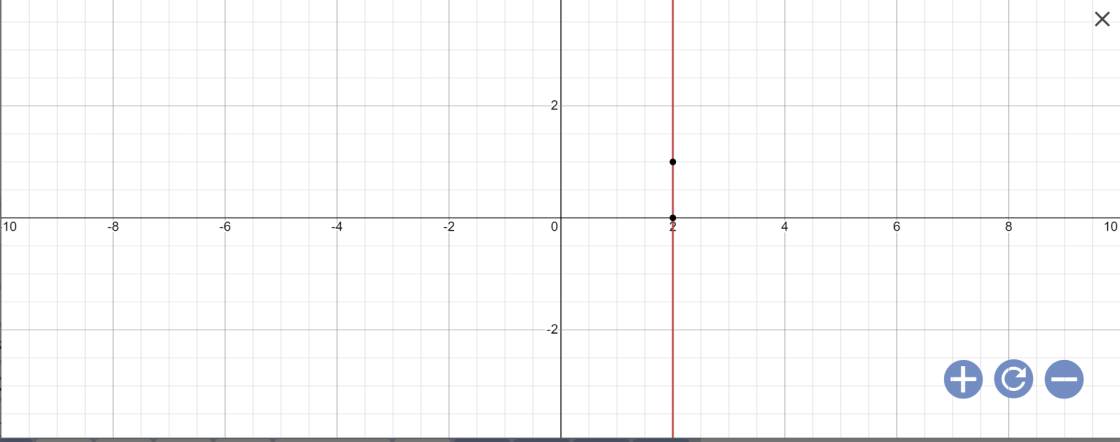
d: 2x+0y=4
=>2x=4
=>x=2
vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x=2\\y\in R\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho 69,6g MnO2 tác dụng với dung dịch HCl đặc, dư. Dẫn khí thoát ra đi vào 500ml dung dịch KOH 4M ở điều kiện thường a) Viết phương trình hóa học của phản ứng xảy ra. chỉ rõ chất khử chất oxi hoá b) Xác định nồng độ mol/l của những chất có trong dung dịch sau phản ứng. Biết rằng tinh thể của dung dịch sau phản ứng thay đổi không đáng kể
\(n_{MnO_2}=\dfrac{69,6}{87}=0,8\left(mol\right)\)
\(MnO_2+4HCl_đ\underrightarrow{t^o}MnCl_2+2Cl_2+2H_2O\)
0,8------------------------------>1,6
Chất oxi hóa là \(MnO_2\)
\(Mn^{+4}+2e\rightarrow Mn^{+2}\)
Chất khử là HCl
\(Cl^{-1}\rightarrow Cl^0+2e\)
\(n_{KOH}=0,5.4=2\left(mol\right)\)
\(3Cl_2+2KOH\rightarrow KCl+KClO+H_2O\)
0,8--->\(\dfrac{8}{15}\)------->\(\dfrac{4}{15}\)---->\(\dfrac{4}{15}\)
\(CM_{KOH}=\dfrac{2-\dfrac{8}{15}}{0,5}=2,93M\)
\(CM_{KCl}=\dfrac{\dfrac{4}{15}}{0,5}=0,5M\\ CM_{KClO}=\dfrac{\dfrac{4}{15}}{0,5}=0,5M\)
Đúng 0
Bình luận (1)
Hai người cùng làm một công việc trong 12 giờ thì xong nếu người thứ nhất làm một mình được nửa công việc và để người thứ hai làm phần còn lại cho xong thì mất tất cả 25 ngày. Hỏi mỗi người làm một mình thì bao lâu sẽ xong
a:
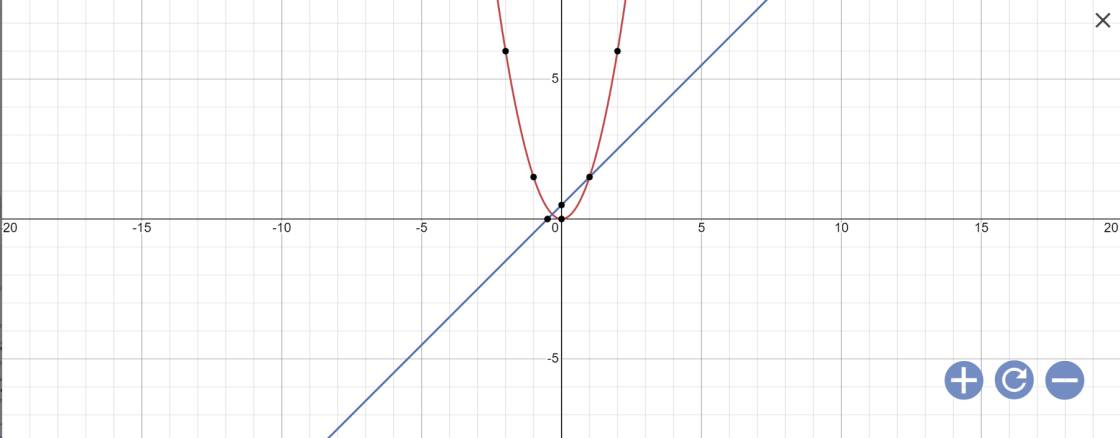
b: Phương trình hoành độ giao điểm là:
\(\dfrac{3}{2}x^2=x+\dfrac{1}{2}\)
=>\(3x^2=2x+1\)
=>\(3x^2-2x-1=0\)
=>(x-1)(3x+1)=0
=>\(\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Khi x=1 thì \(y=\dfrac{3}{2}\cdot1^2=\dfrac{3}{2}\)
Khi x=-1/3 thì \(y=\dfrac{3}{2}\cdot\left(-\dfrac{1}{3}\right)^2=\dfrac{3}{2}\cdot\dfrac{1}{9}=\dfrac{1}{6}\)
Vậy: Tọa độ giao điểm là \(A\left(1;\dfrac{3}{2}\right);B\left(-\dfrac{1}{3};\dfrac{1}{6}\right)\)
c: Phương trình hoành độ giao điểm là:
\(\dfrac{3}{2}x^2=x+m\)
=>\(\dfrac{3}{2}x^2-x-m=0\)
\(\text{Δ}=\left(-1\right)^2-4\cdot\dfrac{3}{2}\cdot\left(-m\right)=1+6m\)
Để (D) cắt (P) tại hai điểm phân biệt thì Δ>0
=>6m+1>0
=>m>-1/6
Để (D) tiếp xúc với (P) thì Δ=0
=>6m+1=0
=>m=-1/6
Để (D) không cắt (P) thì Δ<0
=>6m+1<0
=>m<-1/6
Đúng 0
Bình luận (0)
\(A=\dfrac{3x^2-11x-14}{4x^2+7x+3}=\dfrac{3x^2+3x-14x-14}{4x^2+4x+3x+3}=\dfrac{3x\left(x+1\right)-14\left(x+1\right)}{4\left(x+1\right)+3\left(x+1\right)}\\ =\dfrac{\left(x+1\right)\left(3x-14\right)}{\left(x+1\right).\left(4+3\right)}=\dfrac{3x-14}{7}\)
\(B=\dfrac{x^2+13x-7x-91}{x^2+15x-7x-105}=\dfrac{x\left(x+13\right)-7\left(x+13\right)}{x\left(x+15\right)-7\left(x+15\right)}=\dfrac{\left(x-7\right)\left(x+13\right)}{\left(x-7\right)\left(x+15\right)}\\ =\dfrac{x+13}{x+15}\)
Đúng 0
Bình luận (0)
\(C=\dfrac{x^3-6x^2+11x-6}{x^2-3x+2}=\dfrac{x^3-3x^2+2x-3x^2+9x-6}{x^2-3x+2}\\ =\dfrac{x\left(x^2-3x+2\right)-3\left(x^2-3x+2\right)}{x^2-3x+2}=\dfrac{\left(x-3\right)\left(x^2-3x+2\right)}{x^2-3x+2}=x-3\)
Đúng 0
Bình luận (0)
\(A=\dfrac{3x^2-11x-14}{4x^2+7x+3}\)
\(=\dfrac{3x^2-14x+3x-14}{4x^2+4x+3x+3}\)
\(=\dfrac{x\left(3x-14\right)+\left(3x-14\right)}{\left(x+1\right)\left(4x+3\right)}=\dfrac{\left(x+1\right)\left(3x-14\right)}{\left(x+1\right)\left(4x+3\right)}=\dfrac{3x-14}{4x+3}\)
\(B=\dfrac{x^2+6x-91}{x^2+8x-105}\)
\(=\dfrac{x^2+13x-7x-91}{x^2+15x-7x-105}\)
\(=\dfrac{x\left(x+13\right)-7\left(x+13\right)}{x\left(x+15\right)-7\left(x+15\right)}\)
\(=\dfrac{\left(x+13\right)\left(x-7\right)}{\left(x+15\right)\left(x-7\right)}=\dfrac{x+13}{x+15}\)
\(C=\dfrac{x^3-6x^2+11x-6}{x^2-3x+2}\)
\(=\dfrac{x^3-x^2-5x^2+5x+6x-6}{\left(x-1\right)\left(x-2\right)}\)
\(=\dfrac{\left(x-1\right)\left(x^2-5x+6\right)}{\left(x-1\right)\left(x-2\right)}=\dfrac{x^2-5x+6}{x-2}\)
\(=\dfrac{\left(x-2\right)\left(x-3\right)}{x-2}=x-3\)
Đúng 0
Bình luận (0)
a: Thay x=-2 vào (P), ta được:
\(y=\left(-2\right)^2=4\)
Vậy: A(-2;4)
b: Thay x=0 và y=2022 vào (d), ta được:
\(0+m-1=2022\)
=>m-1=2022
=>m=2023
c: Phương trình hoành độ giao điểm là:
\(x^2=x+m-1\)
=>\(x^2-x-m+1=0\)
\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(-m+1\right)\)
\(=1+4m-4=4m-3\)
Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>4m-3>0
=>4m>3
=>\(m>\dfrac{3}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=-m+1\end{matrix}\right.\)
\(\left(y_1-y_2\right)\left(x_1-x_2\right)=9\)
=>\(\left(x_1^2-x_2^2\right)\left(x_1-x_2\right)=9\)
=>\(\left(x_1+x_2\right)\cdot\left(x_1-x_2\right)^2=9\)
=>\(\left(x_1+x_2\right)^2-4x_1x_2=9\)
=>1-4(-m+1)=9
=>1+4m-4=9
=>4m-3=9
=>4m=12
=>m=3(nhận)
Đúng 0
Bình luận (0)
Bài 3:
a: \(\text{Δ}=\left[-\left(2m+3\right)\right]^2-4\cdot1\cdot m=\left(2m+3\right)^2-4m\)
\(=4m^2+12m+9-4m\)
\(=4m^2+8m+9\)
\(=4m^2+8m+4+5=\left(2m+2\right)^2+5>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+3\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(2m+3\right)^2-2m\)
\(=4m^2+12m+9-2m\)
\(=4m^2+10m+9\)
\(=\left(2m\right)^2+2\cdot2m\cdot2,5+6,25+2,75\)
\(=\left(2m+2,5\right)^2+2,75>=2,75\forall m\)
Dấu '=' xảy ra khi 2m+2,5=0
=>m=-1,25
Bài 2:
a: \(x_1+x_2=3+2=5;x_1x_2=3\cdot2=6\)
Phương trình lập được sẽ là \(A^2-5A+6=0\)
b: \(x_1+x_2=\dfrac{3}{5}+2=2,6;x_1x_2=\dfrac{3}{5}\cdot2=\dfrac{6}{5}=1,2\)
Phương trình lập được sẽ là:
\(A^2-2,6A+1,2=0\)
Đúng 0
Bình luận (0)