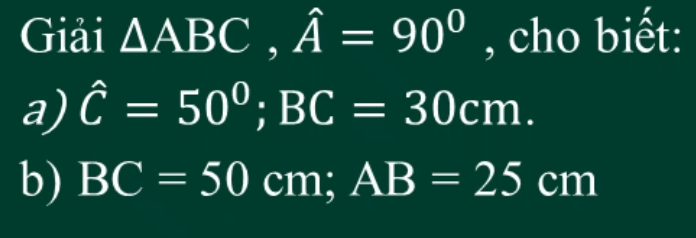Nêu một cách ngắn gọn về tâm trạng của pê-nê-lốp khi thử thách uy lit xo
Nghị luận về công tác phòng chống dịch của em trong mùa covid
Ca2 : 2 là phân tử khối đúng không
ở phép lai đực AA lai với cái  phát sinh ra ở F1 1 thể đột biến. a) F1 có kiểu gen AAa. b) F1 có kiểu gen AAAa. c) F1 có kiểu gen Aaa. Xác định bộ NST có thể có ở 3 trường hợp trên. Cơ chế phát sinh của mỗi trường hợp
Đọc tiếp
smile peer yell stroll stare hiss wander rush laugh whisper25.Rosie’s such a cheerful girl because she always ........... to us. (1 Point) Enter your answer26.The house seemed empty, but I ………. through the window to see if anybody was there. (1 Point) Enter your answer27.The children ran away when they heard their mother ……….. (1 Point) Enter your answer28.I ……….. along the beach with the warm sun on my face. (1 Point) Enter your answer29.The children …………… a...
Đọc tiếp
smile peer yell stroll stare hiss wander rush laugh whisper
25.Rosie’s such a cheerful girl because she always ........... to us. (1 Point) Enter your answer
26.The house seemed empty, but I ………. through the window to see if anybody was there. (1 Point) Enter your answer
27.The children ran away when they heard their mother ……….. (1 Point) Enter your answer
28.I ……….. along the beach with the warm sun on my face. (1 Point) Enter your answer
29.The children …………… at the old lady’s strange hat. (2 Points) Enter your answer
30.The boy …………. a warning to be quiet. (1 Point) Enter your answer
31.For an hour or two, we …………. around the city, totally lost. (1 Point) Enter your answer
32.Try to do your work calmly and carefully, without ………… (2 Points) Enter your answer
33.I always …………….. at Andrew’s silly jokes. (2 Points) Enter your answer
34.The child was ……………… in her mother’s ear so that no one else could hear he
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.a) Chứng minh rằng AD + BE DEb) AC cắt DO tại M, BC cắt OE tại N. Tứ giác CMON là hình gì? Vì sao?c/ Chứng minh: MO.MD+ON.NE không đổid) AN cắt CO tại điểm H. Điểm H di chuyển trên đường nào khi C di chuyển trên nửa đường tròn (O; R).
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
a) Chứng minh rằng AD + BE = DE
b) AC cắt DO tại M, BC cắt OE tại N. Tứ giác CMON là hình gì? Vì sao?
c/ Chứng minh: MO.MD+ON.NE không đổi
d) AN cắt CO tại điểm H. Điểm H di chuyển trên đường nào khi C di chuyển trên nửa đường tròn (O; R).
Giải giùm mình
Câu 2. Đơn giản biểu thức : a . AD + CK - AF - CD b . OM - ON + AD + MA + EK - ED