a) (x^2 +2x+1)-x-1 phần 3=6(x+1)^2-5x-5 phần 6
b)(x-1)-2(x-1) phần 3=1 + (2x-2) phần 2
c)(x-2)^2=(2x-3)^2-(x+1)^2
d)(x-2)(x^2-3x+5)=x^2-2x^2
a) (x^2 +2x+1)-x-1 phần 3=6(x+1)^2-5x-5 phần 6
b)(x-1)-2(x-1) phần 3=1 + (2x-2) phần 2
c)(x-2)^2=(2x-3)^2-(x+1)^2
d)(x-2)(x^2-3x+5)=x^2-2x^2
b: \(\left(x-1\right)-\dfrac{2\left(x-1\right)}{3}=1+\dfrac{\left(2x-2\right)}{2}\)
=>\(\dfrac{1}{3}\left(x-1\right)-\left(x-1\right)=1\)
=>\(\dfrac{-2}{3}\left(x-1\right)=1\)
=>\(x-1=1:\dfrac{-2}{3}=\dfrac{-3}{2}\)
=>\(x=-\dfrac{3}{2}+1=-\dfrac{1}{2}\)
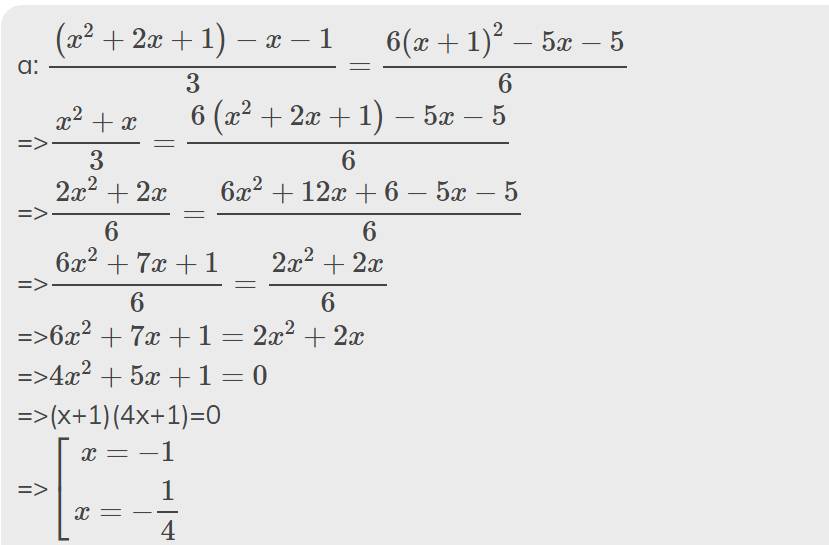
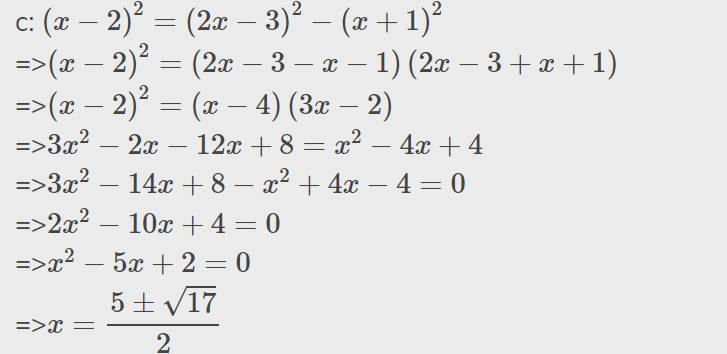
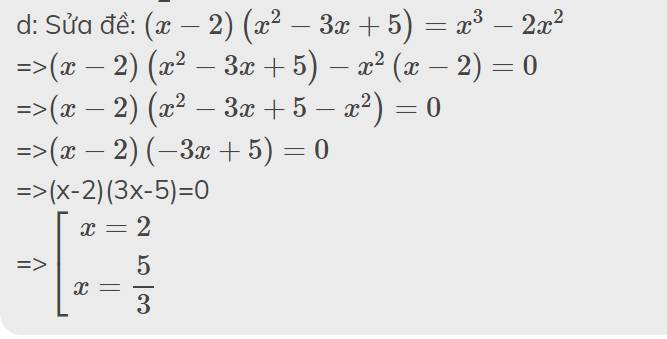
a) (2x+1)^2+(x+3)^2=5(x+7)(x-7)
b)(x-3)^2-2(x-1)=6x(x-2)-5x^2
c)(x+2)^2-(x-2)^3=12x(x-2)-8
phương trình bặc nhé
`a) (2x+1)^2+(x+3)^2=5(x+7)(x-7)`
`<=> 4x^2 + 4x + 1 + x^2 +6x +9 = 5(x^2 -49)`
`<=> 5x^2 + 10x +10 = 5x^2 - 245`
`<=> 10x = 255`
`<=> x=25,5`
`b)(x-3)^2-2(x-1)=6x(x-2)-5x^2`
`<=> x^2 - 6x + 9 -2x +2 = 6x^2 - 12x -5x^2`
`<=> -6x +12x -2x = -11`
`<=> 4x =-11`
`<=> x=-11/4`
Giải phương trình sau:
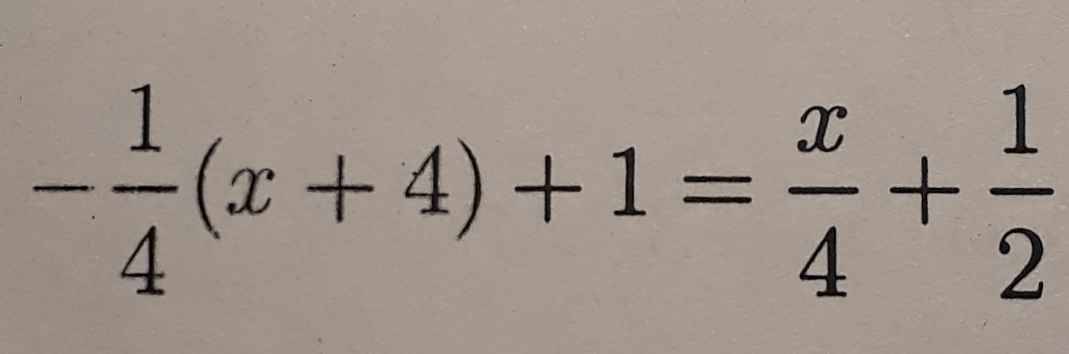
\(-\dfrac{1}{4}\left(x+4\right)+1=\dfrac{x}{4}+\dfrac{1}{2}\)
\(\Leftrightarrow-\dfrac{1}{4}x-1+1-\dfrac{x}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow-\dfrac{x}{4}-\dfrac{x}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow-\dfrac{2x}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow-\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow x=-1\)
#Urushi
=>-1/4x-1+1=x/4+1/2
=>-1/4x-1/4x=1/2
=>-1/2x=1/2
=>x=-1
Lời giải:
$P=2(x^2+y^2-xy)+3x^2+2x-8y+2034$
$=2(x-y)^2+8(x-y)+3x^2-6x+2034$
$=2[(x-y)^2+4(x-y)+4]+3(x^2-2x+1)+2023$
$=2(x-y+2)^2+3(x-1)^2+2023\geq 2023$
Vậy $P_{\min}=2023$. Giá trị này đạt tại $x-y+2=x-1=0$
$\Leftrightarrow x=1; y=3$
a: Xét ΔBAD và ΔBCD có
BA=BC
góc ABD=góc CBD
BD chung
=>ΔBAD=ΔBCD
=>DA=DC và góc BDA=góc CDA
=>DB là phân giác của góc ADC
b: góc DBE=90 độ
góc DBA=45 độ
=>góc ABE=90-45=45 độ
Xét ΔBDA và ΔBEA có
BD=BE
góc DBA=góc EBA
BA chung
=>ΔBDA=ΔBEA
=>AD=AE=CD
góc DCB+góc AEB=45+45=90 độ
=>EA vuông góc CD
a) tính hợp lý
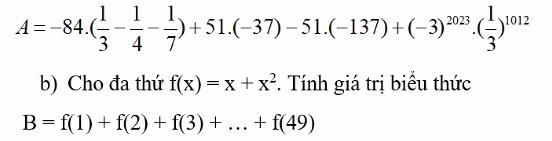
a: =-84*(28/84-21/84-12/84)+51(-37+137)-3^2023*1/3^1012
=5+5100-3^1011
=-3^2011+5105
b: B=1+2+...+49+1^2+2^2+...+49^2
=49*50/2+49(49+1)(2*49+1)/6
=41650
tìm x,y,z biết:
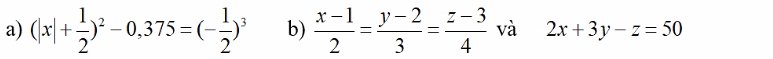
a: =>(|x|+1/2)^2=-1/8+3/8=1/4
=>|x|+1/2=1/4 hoặc |x|+1/2=-1/4(loại)
=>|x|=1/4-1/2=-1/4(loại)
b: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{2x+3y-z-2-6+3}{2\cdot2+3\cdot3-4}=5\)
=>x-1=10 và y-2=15 và z-3=20
=>x=11 và y=17 và z=23
Lời giải:
$P=(4x^2+y^2-4xy)+x^2+14x-4y+2015$
$=(2x-y)^2+4(2x-y)+(x^2+6x)+2015$
$=(2x-y)^2+4(2x-y)+4+(x^2+6x+9)+2002$
$=(2x-y+2)^2+(x+3)^2+2002\geq 2002$
Vậy $P_{\min}=2002$. Giá trị này đạt tại $2x-y+2=x+3=0$
$\Leftrightarrow x=-3; y=-4$
giúp mik vs ạ mình cần phương pháp để giải ạ
mik ko cần đáp án
một người đi xe máy từ A đến B với vận tốc 40km/h. Lúc về, người đó đi với vận tốc 30km/h, nên thời gian đi về nhiều hơn thời gian đi là 45 phút. Tình quãng đường AB
Gọi a là thời gian lúc đi của người đó (h) (a>0)
Đổi 45p=0,75h
Quãng đường lúc đi là 40a (km); Quãng đường khi về là 30(a+0,75) (h)
Vì cùng là quãng đường AB nên ta có:
40a= 30(a+0,75)
<=> 40a - 30a = 22,5
<=> 10a = 22,5
<=>a= 2,25(TM)
Vậy quãng đường AB dài: 40a= 40.2,25=90(km)