a) Tìm điều kiện để các căn thức sau có nghĩa: căn x-10 b) đưa thừa số ra ngoài dấu căn: a cân9²b(a>_0) c) so sánh: 2căn3+1 và 2căn2+căn5
Ôn tập Hệ thức lượng trong tam giác vuông
a: ĐKXĐ: x-10>=0
=>x>=10
b: \(\sqrt{9a^2b}=\sqrt{\left(3a\right)^2\cdot b}=3a\cdot\sqrt{b}\)
c: \(\left(2\sqrt{3}+1\right)^2=13+4\sqrt{3}\)
\(\left(2\sqrt{2}+\sqrt{5}\right)^2=8+5+2\cdot2\sqrt{2}\cdot\sqrt{5}=13+4\sqrt{10}\)
mà \(4\sqrt{3}< 4\sqrt{10}\left(3< 10\right)\)
nên \(\left(2\sqrt{3}+1\right)^2< \left(2\sqrt{2}+\sqrt{5}\right)^2\)
=>\(2\sqrt{3}+1< 2\sqrt{2}+\sqrt{5}\)
Đúng 3
Bình luận (0)
Trục căn thức ở mẫu a) Căn5/căn7 b)2/căn a-1(với a>_ 0 và a khác 1)
a: \(\dfrac{\sqrt{5}}{\sqrt{7}}=\dfrac{\sqrt{5\cdot7}}{7}=\dfrac{\sqrt{35}}{7}\)
b: \(\dfrac{2}{\sqrt{a}-1}=\dfrac{2\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}=\dfrac{2\sqrt{a}+2}{a-1}\)
Đúng 1
Bình luận (0)
Rút gọn các biểu thức sau a) 3cân20-cân45+cân75 b) (cân50-2cân18+cân98):cân2
a: \(3\sqrt{20}-\sqrt{45}+\sqrt{75}\)
\(=3\cdot2\sqrt{5}-3\sqrt{5}+5\sqrt{3}\)
\(=6\sqrt{5}-3\sqrt{5}+5\sqrt{3}=3\sqrt{5}+5\sqrt{3}\)
b: \(\dfrac{\left(\sqrt{50}-2\sqrt{18}+\sqrt{98}\right)}{\sqrt{2}}\)
\(=\dfrac{5\sqrt{2}-2\cdot3\sqrt{2}+7\sqrt{2}}{\sqrt{2}}\)
=5-6+7
=12-6
=6
Đúng 1
Bình luận (0)
Cho biểu thức: A=15cân4a+cân a-cân25a a) rút gọn A b) tính giá trị của biểu thức A tại A=100 b) Vẽ AM là đường trung tuyến của tam giác ABC (M thuộc BC) . Chứng minh góc BAH= góc MAC c) Vẻ HE vuông góc AB (E thuộc AB), HF vuông góc AC (F thuộc AC) . Chứng minh EF vuông góc AM tại K và tính độ dài AK
Câu 1:
a: \(A=15\sqrt{4a}+\sqrt{a}-\sqrt{25a}\)
\(=15\cdot2\sqrt{a}+\sqrt{a}-5\sqrt{a}\)
\(=30\sqrt{a}-4\sqrt{a}=26\sqrt{a}\)
b: Sửa đề: Khi a=100
Thay a=100 vào A, ta được:
\(A=26\cdot\sqrt{100}=26\cdot10=260\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, góc C=30°, BC=12cm, giải tam giác ABC.
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}+30^0=90^0\)
=>\(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{12}=sin30=\dfrac{1}{2}\)
=>AB=6(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=144-36=108\)
=>\(AC=6\sqrt{3}\left(cm\right)\)
Đúng 2
Bình luận (2)
ABC vuông tại A
⇒ ∠B + ∠C = 90⁰
⇒ ∠B = 90⁰ - ∠C
= 90⁰ - 30⁰
= 60⁰
sinB = AC/BC
⇒ AC = BC . sinB
= 12 . sin60⁰
= 6√3 (cm)
sinC = AB/BC
⇒ AB = BC.sinC
= 12.sin30⁰
= 6 (cm)
Đúng 2
Bình luận (0)
Cho tam giác MNP vương tại M, viết các tí số lượng giác của góc N?
Xét ΔMNP vuông tại M có
\(sinN=\dfrac{MP}{NP}\)
\(cosN=\dfrac{MN}{NP}\)
\(tanN=\dfrac{MP}{MN}\)
\(cotN=\dfrac{NM}{MP}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=6cm. AC=8cm a) Tính BC,AH, góc B,góc C b) Vẽ AM là đường trung tuyến của tam giác ABC (M thuộc BC) . Chứng minh góc BAH= góc MAC c) Vẻ HE vuông góc AB (E thuộc AB), HF vuông góc AC (F thuộc AC) . Chứng minh EF vuông góc AM tại K và tính độ dài AK
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC=MB=BC/2
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\left(1\right)\)
\(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAB}+\widehat{ABH}=90^0\)(ΔABH vuông tại H)
Do đó: \(\widehat{ACB}=\widehat{HAB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MAC}=\widehat{HAB}\)
c: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>\(\widehat{AFE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AFE}=\widehat{ABC}\)
\(\widehat{AFE}+\widehat{MAC}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>FE vuông góc AM tại K
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(HA^2=AE\cdot AB\)
=>\(AE\cdot6=4,8^2\)
=>\(AE=3,84\left(cm\right)\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
=>\(AF=\dfrac{4.8^2}{8}=2,88\left(cm\right)\)
Xét ΔAEF vuông tại A có AK là đường cao
nên \(\dfrac{1}{AK^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)
=>\(\dfrac{1}{AK^2}=\dfrac{1}{2,88^2}+\dfrac{1}{3.84^2}\)
=>AK=2,304(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC. a) Viết tỉ số lượng giác góc B của AABC. b) Cho AB=6cm, AC = 8cm . Tính BC,AH c ) Chứng minh: AE.AB = AF AC
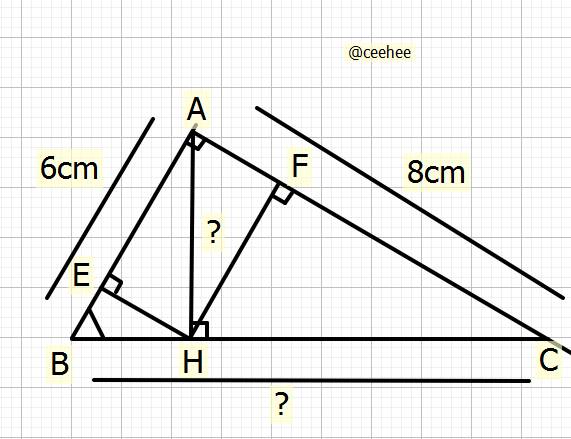
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)
Đúng 1
Bình luận (0)
Cho tam giác vuông ABC vuông tại a AB bé hơn AC có đường cao AH (H thuộc BC) AB = 3 BH =1,8 A) tính BC AH AC B) kẻ HD vuông AC (D thuộc AC) chứng minh HC = AD.AC/HB C) gọi e là điểm đối xứng với H qua AB. Chứng minh S tam giác AED = sin²AHD . S tam giác ACE
cho mạch như hình vễ bt hiệu điện thế giữa hai đầu đoạn mạch AB là 24V điện trở R1=15 Ω, R2=R3=10 Ω
a)tính điện trở Tương đương của đoạn mạch AB?
b)CĐDĐ chạy qua đoạn mạch AB và chạy qua các diện trở
(ghi chú: R2,R1 đoạn mạch ss;R3 đoạn mạch nối tiếp)
Bạn cho mình xin hình vẽ nha bạn
Đúng 0
Bình luận (0)