Cho b2 = a.c. CM rằng a2 + b2 / b2 + c2 = a/c
Ôn tập chương 1
\(\dfrac{a^2+b^2}{b^2+c^2}=\dfrac{a^2+ac}{ac+c^2}=\dfrac{a\left(a+c\right)}{c\left(a+c\right)}=\dfrac{a}{c}\left(đpcm\right)\)
Đúng 3
Bình luận (2)
Thay b2 = ac vào biểu thức trên, ta có:
\(\dfrac{a^2+ac}{ac+c^2}=\dfrac{a\left(a+c\right)}{c\left(a+c\right)}=\dfrac{a}{c}\)
\(\Rightarrow\dfrac{a^2+b^2}{b^2+c^2}=\dfrac{a}{c}\)
Đúng 2
Bình luận (0)
\(b^2=ac\Leftrightarrow\dfrac{a}{b}=\dfrac{b}{c}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{a^2}{b^2}=\dfrac{b^2}{c^2}=\dfrac{a^2+b^2}{b^2+c^2}\left(1\right)\)
Ta có \(b^2=ac\Leftrightarrow\dfrac{ac}{c^2}=\dfrac{b^2}{c^2}\Leftrightarrow\dfrac{a}{c}=\dfrac{b^2}{c^2}\left(2\right)\)
\(\left(1\right)\left(2\right)\LeftrightarrowĐpcm\)
Đúng 2
Bình luận (1)
Lời giải:
Hệ số tỉ lệ của $x,y$ là: $\frac{3}{7}.\frac{35}{6}=\frac{5}{2}$
Đáp án D.
Đúng 1
Bình luận (0)
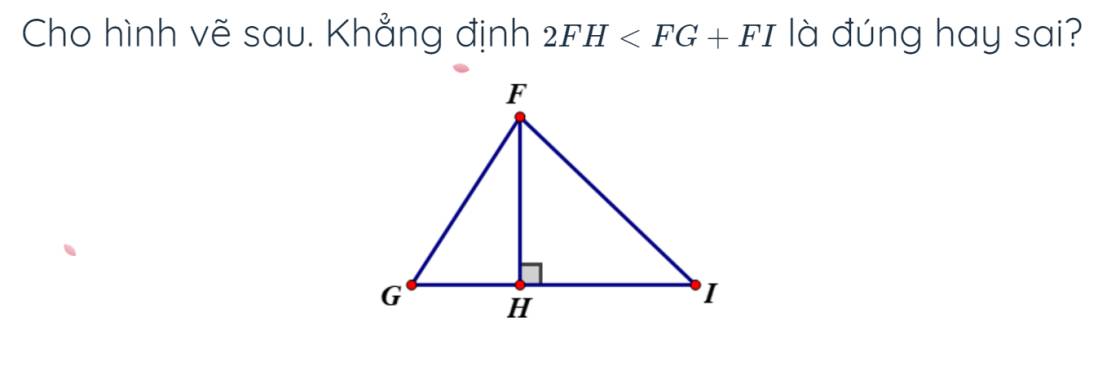
Do \(FH\) là đường vuông góc hạ từ \(F\) đến \(GI\)
\(\Rightarrow FH< FG\)
\(FH< FI\)
Cộng vế với vế ta có:
\(FH+FH< FG+FI\)
Hay \(2FH< FG+FI\)
Vậy khẳng định trên là đúng
Đúng 1
Bình luận (0)
x và y tỉ lệ thuận với nhau
=>\(y=a\cdot x\)
=>-1=3a
=>\(a=-\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
ta có tỉ lệ thức là
-3x=5y=>\(\dfrac{-3}{5}=\dfrac{y}{x}\)
Đúng 1
Bình luận (0)
y tỉ lệ thuận với x theo hệ số tỉ lệ là a=7
=>y=7x
=>\(x=\dfrac{1}{7}y\)
Đúng 1
Bình luận (0)
x và y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{2x_1-3x_2}{2y_1-2y_2}=\dfrac{42.5}{-8.5}=-5\)
=>x=-5y
Đúng 1
Bình luận (0)
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{a-b}{2-3}=\dfrac{-5}{-1}=5\)
\(\Rightarrow\left\{{}\begin{matrix}a=2.5=10\\b=3.5=15\end{matrix}\right.\)
\(\Rightarrow a+2b=40\)
Đúng 1
Bình luận (1)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{a-b}{2-3}=\dfrac{-5}{-1}=5\)
=>\(a=5\cdot2=10;b=5\cdot3=15\)
a+2b=10+2*15=40
Đúng 0
Bình luận (0)
Bài 1: Cô Lan mua hai món hàng ở một siêu thị: Món hàng thứ nhất giá 300 000 đồng và được giảm giá 10%; món hàng thứ hai được giảm giá 15%. Tổng số tiền cô Lan phải thanh toán cho siêu thị là 842 500 đồng. Hỏi giá tiền món hàng thứ hai lúc chưa giảm giá là bao nhiêu?
Đọc tiếp
Bài 1: Cô Lan mua hai món hàng ở một siêu thị: Món hàng thứ nhất giá 300 000 đồng và được giảm giá 10%; món hàng thứ hai được giảm giá 15%. Tổng số tiền cô Lan phải thanh toán cho siêu thị là 842 500 đồng. Hỏi giá tiền món hàng thứ hai lúc chưa giảm giá là bao nhiêu?
Giá tiền của món thứ nhất là:
\(300000\left(1-10\%\right)=270000\left(đồng\right)\)
Số tiền phải trả cho món hàng thứ hai là:
\(842500-270000=572500\left(đồng\right)\)
Giá tiền niêm yết của món hàng thứ hai là:
\(572500:\left(1-15\%\right)\simeq673529,4118\left(đồng\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC . Gọi M là trung điểm của BC . Quá B và C lần lượt kẻ BD và CE vuông góc với đường thẳng AM a. Chứng minh BD= CE và BD // CE b. Chứng minh BE // CD và BE = CD c. Chứng minh AD + AE = 2AM
a: Xét ΔBMD vuông tại D và ΔCME vuông tại E có
MB=MC
\(\widehat{BMD}=\widehat{CME}\)(hai góc đối đỉnh)
Do đó: ΔBMD=ΔCME
=>BD=CE
Ta có: BD\(\perp\)AM
CE\(\perp\)AM
Do đó: BD//CE
b: Xét tứ giác BDCE có
BD//CE
BD=CE
Do đó: BDCE là hình bình hành
=>BE//CD và BE=CD
c: \(AD+AE=AD+AD+DE\)
\(=2AD+2DM\)
\(=2\left(AD+DM\right)=2AM\)
Đúng 1
Bình luận (1)