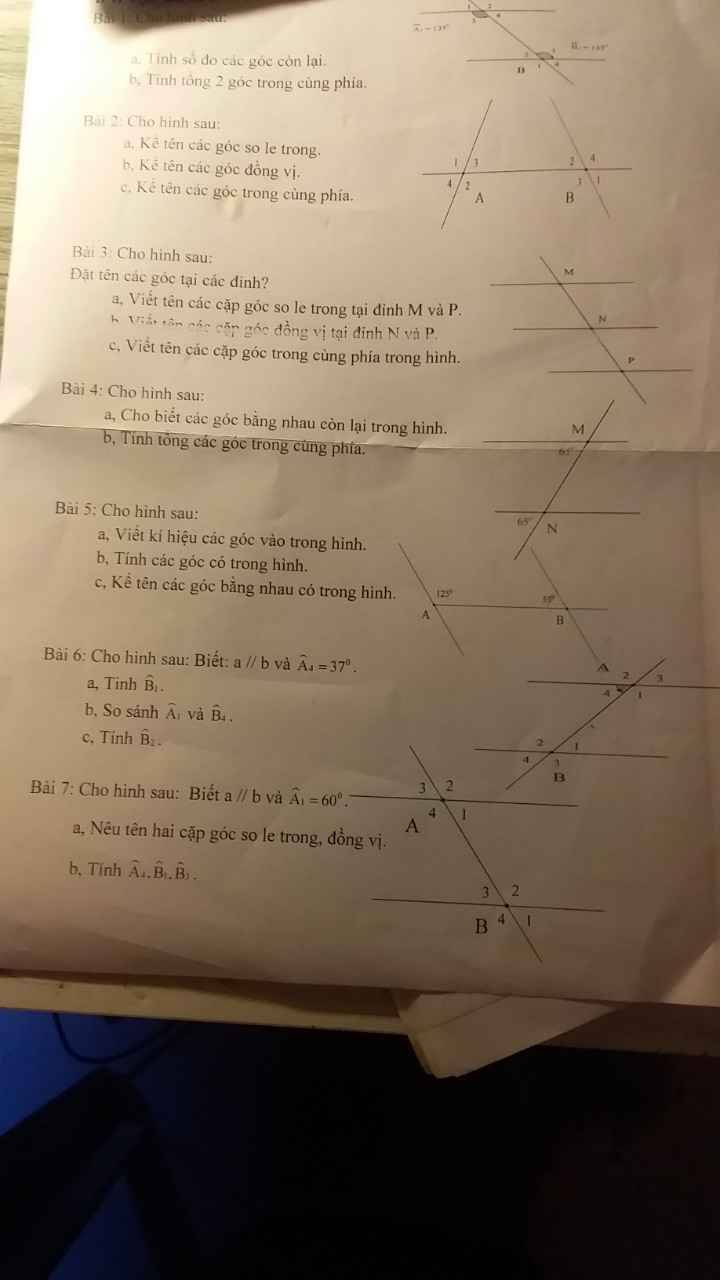Ai giúp giải với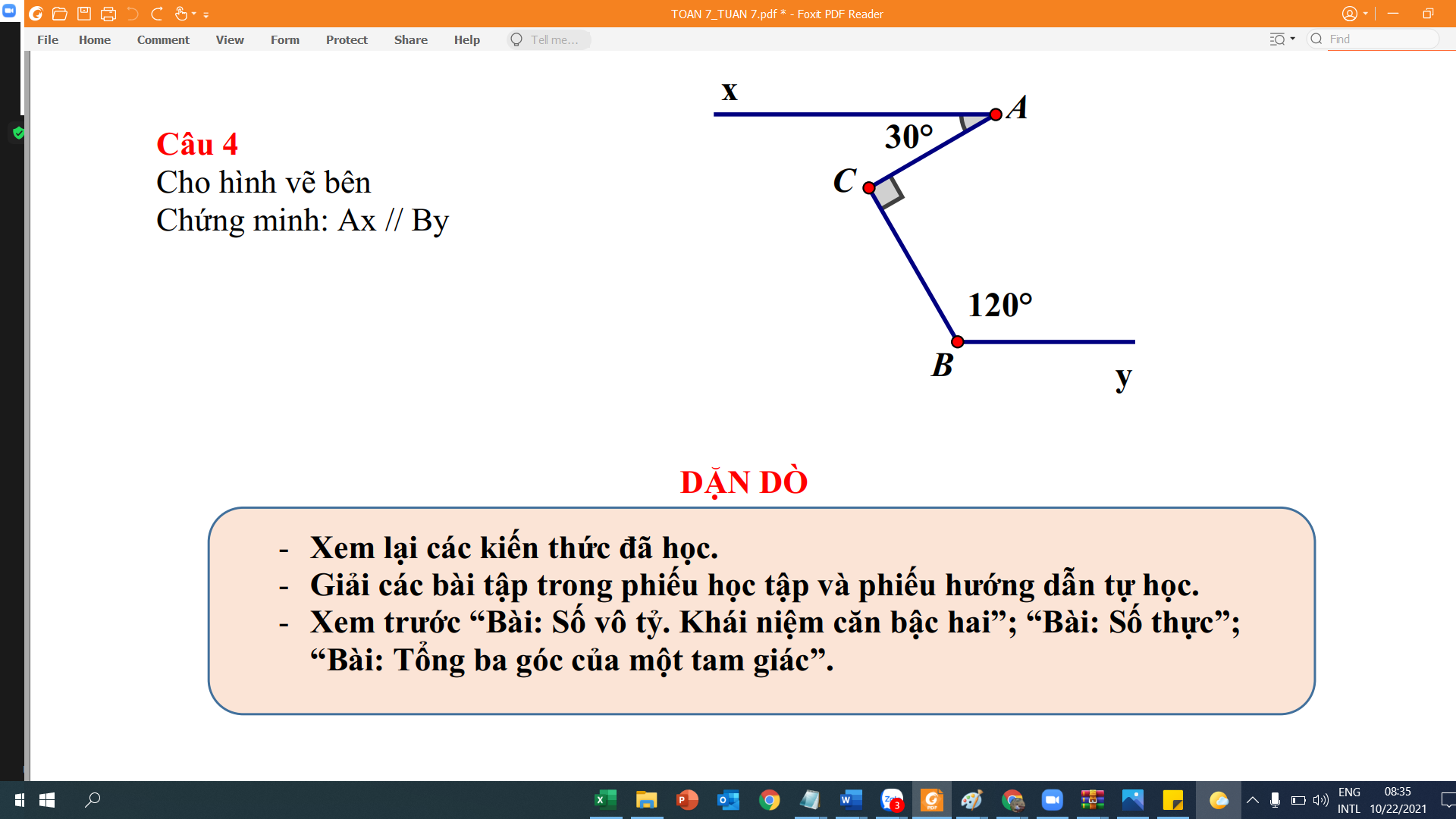
Ôn tập chương Đường thẳng vuông góc. Đường thẳng song song
Kẻ Cz//Ax
\(\Rightarrow\widehat{ACz}=\widehat{CAx}=30^0\)(so le trong)
\(\Rightarrow\widehat{BCz}=\widehat{ACB}-\widehat{ACz}=90^0-30^0=60^0\)
Ta có: \(\widehat{BCz}+\widehat{CBy}=60^0+120^0=180^0\)
Mà 2 góc này trong cùng phía
=> Cz//By
Mà Cz//Ax
=> Ax//By
Đúng 2
Bình luận (0)
Cho hình sau. Biết BF vuông góc EF, góc ABC + góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
+ góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
Xem chi tiết
 + góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
+ góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
Bài 7:
a) Hai cặp góc so le trong là:
\(\widehat{A_1}\) và \(\widehat{B_3}\)
\(\widehat{A_4}\) và \(\widehat{B_2}\)
b) Ta có:
\(\widehat{A_1}+\widehat{A_4}=180^o\) (kề bù)
\(\Rightarrow\widehat{A_4}=180^o-60^o=120^o\)
Mà: \(\widehat{B_1}=\widehat{A_1}=60^o\) (đồng vị)
Và: \(\widehat{B_1}\) đối đỉnh \(\widehat{B_3}\)
\(\Rightarrow\widehat{B_3}=\widehat{B_1}=60^o\)
Đúng 1
Bình luận (0)
6:
a: a//b
=>góc A4=góc B1(hai góc so le trong)
=>góc B1=37 độ
b: góc B4=góc B1=37 độ
góc A1+góc A4=180 độ
=>góc A1=180-37=143 độ
=>góc B4<góc A1
c: góc B4+góc B2=180 độ(kề bù)
=>góc B2=180-37=143 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc BAC=135 độ.Về phía ngoài tam giác ABC,dựng các tam giác vuông cân ABD và ACE.Gọi K là giao điểm của BD và CE.Chứng minh rằng AK vuông góc BC
Cho Tam giác ABC vuông tại A,BD là phân giác của ABC (D thuộc Ac) Trên cạnh BC lấy điểm E sao cho BE=BA a. Chứng minh AD=DE b. Trên tia đối của tia AB lấy điểm F sao cho AF=EC chứng minh BD vg với FC c. Chứng minh AE song song với FC d. Chứng minh 3 đ D,E,F thẳng hàng ;-; ai cứu t zới nhanh lên ạ
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đo: ΔBAD=ΔBED
=>DA=DE
b,c: Xét ΔBFC có BA/AF=BE/EC
nên AE//FC
BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
=>BD vuông góc với FC
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
Do đó: ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>D,E,F thẳng hàng
Đúng 1
Bình luận (1)
Nhanh giúp mik vs ạ m cảm ơn 
Do m//n
=>B1=A1=80(hai góc so le trong)
B1+B2=180(hai góc kề bù)
=>B2=180-80=100
B3=B1=80(hai góc đối đỉnh)
B4=B2=100(hai góc đối đỉnh)
Đúng 0
Bình luận (0)
\(\widehat{A_1}=\widehat{B_3}=80^o\) (đồng vị)
\(\widehat{B_1}=\widehat{B_3}=80^o\) (đối đỉnh)
\(\widehat{B_1}+\widehat{B_2}=180^o\) (kề bù)
\(\Rightarrow\widehat{B_2}=180^o-\widehat{B_1}=180^o-80^o=100^o\)
\(\widehat{B_4}=\widehat{B_2}=100^o\) (đối đỉnh)
Vậy: \(\widehat{B_1}=80^o; \widehat{B_2}=100^o; \widehat{B_3}=80^o; \widehat{B_4}=100^o\)
Đúng 0
Bình luận (0)
Hai đường thẳng AB và CD cắt nhau tại O trong các góc tạo thành có góc AOC=130 độ,Ot là tia phân giác của góc BOC
a)Tính góc COt
b)Tính gó BOC;góc AOD
c)Tính góc DOt
Cần gấp câu trả lời cảm ơn trước ạ.
a: góc BOC=180-130=50 độ
=>góc COt=50/2=25 độ
b: góc AOD=góc BOC=50 độ
c: góc tOD=180-25=155 độ
Đúng 1
Bình luận (0)
B3. Cho tia Oz nằm trong góc vuông xOy, xOz = 2.zOy.
a) Tính zOy b) Vẽ tia Ot là phân giác xOz, tính yết.
c) Tia Oz có phải phân giác góc tây không?
SÓ CẰN GẤP
a: góc zOy=1/3*180=60 độ
b: góc xOt=120/2=60 độ
=>góc tOz=120 độ
c: góc zOy=1/2*góc zOt
nên Oy làphân giác của góc zOt
Đúng 0
Bình luận (0)
một bể nước dạng hình hộp chữ nhattj có chiều dài 3m .Lúc đầu bể không có nước . Sau khi đổ vào bể 120 thùng nước , mỗi thùng chứa 20 lít nước thì mực nước củ bể dâng cao 0,8m
a] tính chiều rộng của bể nước
B] Người ta đổ thêm 60 thùng nước thì đầy bể . Hỏi bể nước cao bao nhiêu mét
Thể tích lượng nước đổ vào :
`120 xx 20= 2400(l) = 2,4m^3`
Chiều rộng bể nước :
`2,4 : (3xx0,8) = 1(m)`
Thể tích của hồ nước :
`2400 + 60 xx 20 = 3600(dm^3) = 3,6m^3`
Chiều cao mực nước :
`3,6 :(3xx0,8) = 1,5(m)`
Ds....
Đúng 0
Bình luận (0)