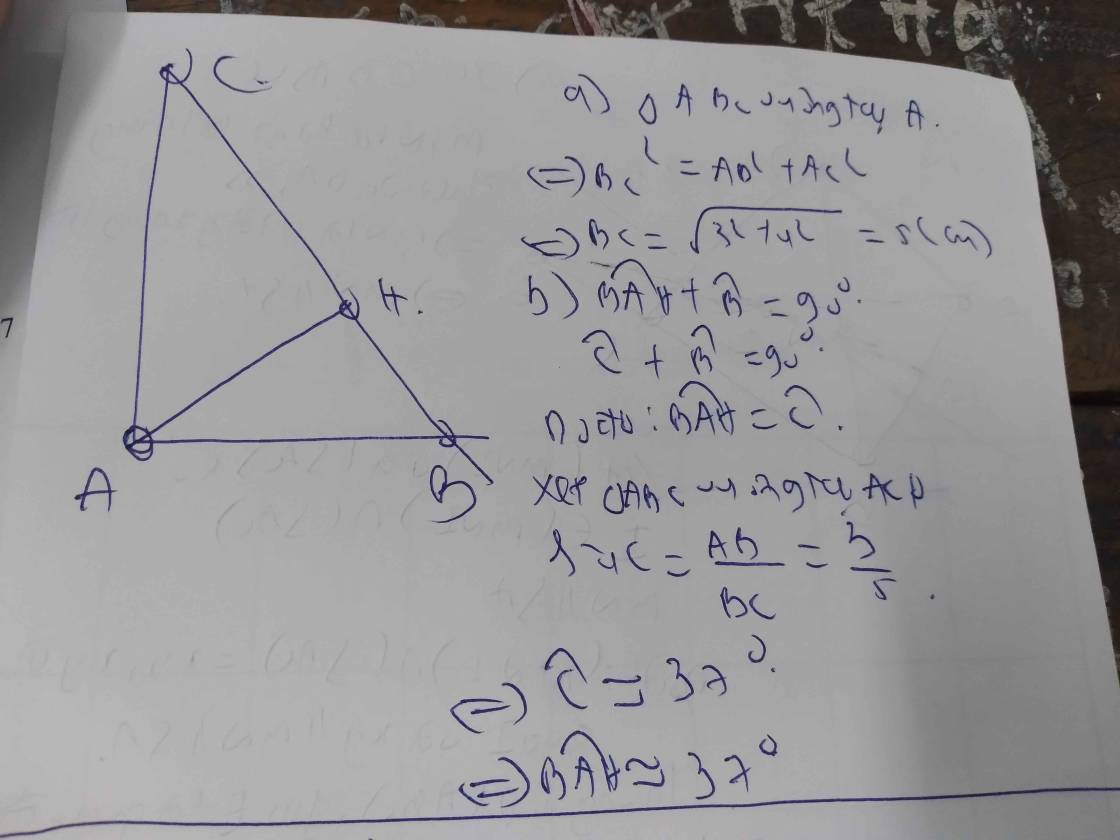
Cho tam giác ABC vuông tại A,kẻ đường cao AH AB=3cm,AC=4cm a)tính BC,AC b)tính góc BAH c)Chứng MINH BH=CH.tan2B
Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
Cho tam giác ABC vuông tại A biết AB = 3cm, AC = 4 cm tính BC, góc B, góc C
\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=3^2+4^2\)
\(=25\)
\(\Rightarrow BC=5\left(cm\right)\)
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\simeq53^0\)
\(\Rightarrow\widehat{C}\simeq90^0-53^0=37^0\)
Đúng 3
Bình luận (0)
Áp dụng định lý Py-ta-go vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Ta có:
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
Mà: \(\widehat{B}+\widehat{C}=90^o\Rightarrow\widehat{C}=90^o-53^o=37^o\)
Vậy: ...
Đúng 1
Bình luận (0)
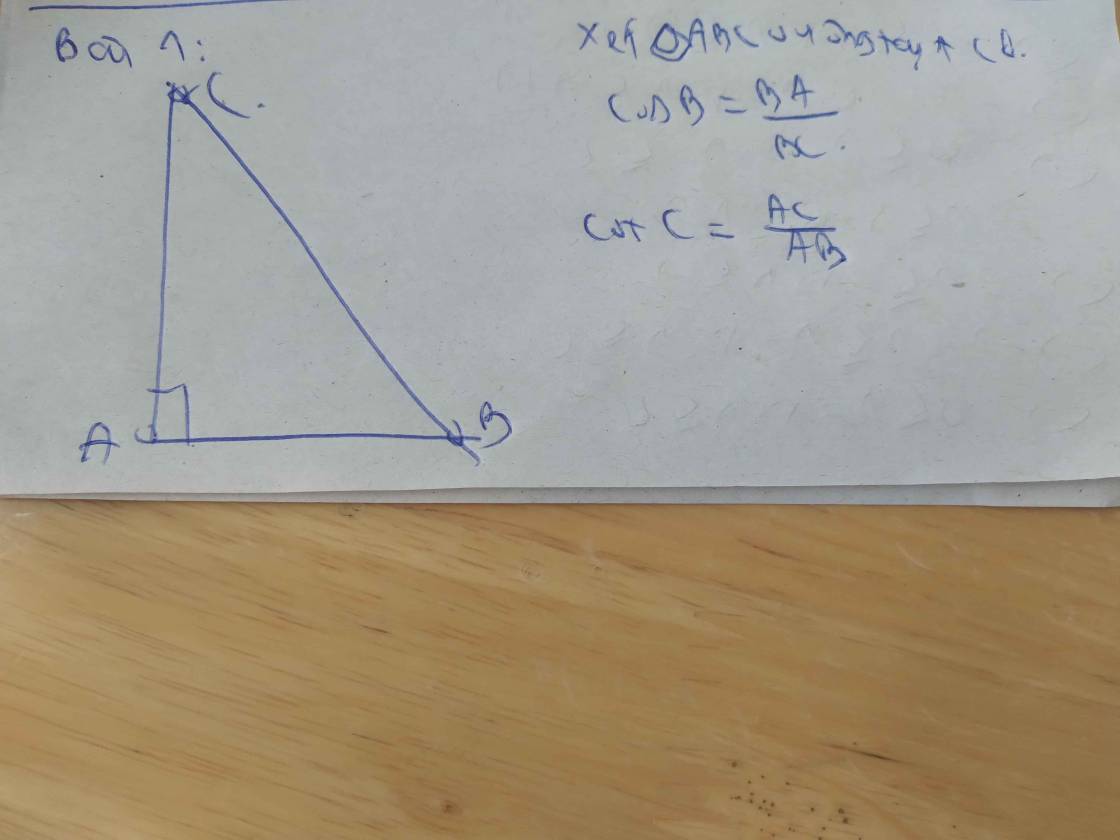
Cho tam giác ABC vuông tại A hãy viết các tỉ số lượng giác của góc B
Các tỉ số lượng giác của góc B là:
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}\\cosB=\dfrac{AB}{BC}\\tanB=\dfrac{AC}{AB}\\cotB=\dfrac{AB}{AC}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bài 1: Cho ∆ABC , BAC = 90° AC= 7cm, BC=15cm.Giải ∆ABC
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(AB^2=15^2-7^2=176\)
=>\(AB=4\sqrt{11}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AC}{BC}=\dfrac{7}{15}\)
=>\(\widehat{C}\simeq28^0\)
=>\(\widehat{B}=90^0-28^0=62^0\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A (AB<AC)đường cao AH (H thuộc BC)
a)Cho AB = 9cm, AC = 12cm. Tính AH,BH,tạc
b)Từ H kẻ HD vuông góc AB tại D, HE vuông góc AC tại E. Chứng minh HD.AB+HE.AC=AB.AC
c)Gọi M là trung điểm BC, AM cắt DE tại I. Chứng minh 1/AI²=1/AD²+1/AE²
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\BH\cdot BC=AB^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=\dfrac{9\cdot12}{15}=7.2\left(cm\right)\\BH=\dfrac{9^2}{15}=5.4\left(cm\right)\end{matrix}\right.\)
b:
ΔAHB vuông tại H có HD là đường cao
nên \(HD\cdot AB=HA\cdot HB\)
ΔAHC vuông tại H có HE là đường cao
nên \(HE\cdot AC=HA\cdot HC\)
\(HD\cdot AB+HE\cdot AC\)
\(=HA\cdot HB+HA\cdot HC=HA\cdot\left(HB+HC\right)\)
\(=HA\cdot BC=AB\cdot AC\)
c: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
ΔABC vuông tại A có AM là trung tuyến
nên AM=MB=MC
\(\widehat{IEA}+\widehat{IAE}=\widehat{DEA}+\widehat{IAC}\)
\(=\widehat{DHA}+\widehat{MCA}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>AM vuông góc DE tại I
ΔADE vuông tại A có AI là đường cao
nên \(\dfrac{1}{AI^2}=\dfrac{1}{AE^2}+\dfrac{1}{AD^2}\)
Đúng 2
Bình luận (0)
a) Ta có:
\(\widehat{C}=90^0-\widehat{A}=90^0-58^0=32^0\)
\(sinB=\dfrac{AC}{BC}\)
\(\Rightarrow AC=BC.sinB=72.sin58^0\approx61,1\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}\)
\(\Rightarrow AB=BC.sinC=72.sin32^0\approx38,2\left(cm\right)\)
b) Ta có:
\(\widehat{C}=90^0-\widehat{B}=90^0-48^0=42^0\)
\(sinB=\dfrac{AC}{BC}\)
\(\Rightarrow BC=\dfrac{AC}{sinB}=\dfrac{20}{sin48^0}=\approx26,9\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}\)
\(\Rightarrow AB=BC.sinC=26,9.sin42^0\approx18\left(cm\right)\)
c) Ta có:
\(\widehat{B}=90^0-\widehat{C}=90^0-30^0=60^0\)
\(sinB=\dfrac{AC}{BC}\)
\(\Rightarrow BC=\dfrac{AC}{sinB}=\dfrac{15}{sin60^0}=10\sqrt{3}\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}\)
\(\Rightarrow AB=BC.sinC=10\sqrt{3}.sin30^0=5\sqrt{3}\left(cm\right)\)
d) Ta có:
\(\widehat{B}=90^0-\widehat{C}=90^0-18^0=72^0\)
\(sinB=\dfrac{AC}{BC}\)
\(\Rightarrow BC=\dfrac{AC}{sinB}=\dfrac{21}{sin72^0}\approx22,1\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}\)
\(\Rightarrow AB=BC.sinC=22,1.sin18^0\approx6,8\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC vuông tại A hãy viết tỉ số lượng giác CosB và cotC Bài 2 :. Cho tam giác ABC vuông tại A có đường cao AK chia cạnh huyền BC thành hai đoạn KB=3 cm và KC=9 cm a) Tỉnh độ dài các đoạn thẳng: BC,AB b) Tính độ dài đoạn thẳng AK c) Trên cạnh AC lấy điểm M ( M khác A và C ). Gọi H là hình chiếu cùa A trên BM. Chứng minh rằng BH .BM=BK . BC
Cho tam giác ABC, biết góc A vuông, góc B=48 độ, cạnh b=20. Độ dài cạnh a là:
Với các giả thiết câu của câu trên, độ dài cạnh c là:
Xét ΔABC vuông tại A
\(sinB=\dfrac{AC}{BC}\\ \Leftrightarrow\sin48=\dfrac{20}{a}\\\Leftrightarrow a=26,9\\BC^2=AC^2+AB^2\\ 29,6^2=20^2+c^2 \\ \Leftrightarrow c^2=476,16\\ \Leftrightarrow c=\sqrt{476,16}=21,8\)
Đúng 2
Bình luận (12)
mọi người ơi em tính ra đáp án 4,901452767 thì làm tròn lên 5 hay chỉ 4,9 thôi vậy
Tuỳ vào bài đó như thế nào
Có những bài có độ chính xác cao em nên giữ nguyên kết quả
Nhưng nguyên tắc làm tròn thì 4,9014 thì làm tròn xuống 4,9 thui chứ không làm tròn lên 5 nha
Đúng 1
Bình luận (0)
Bài 1: Cho tam giác ABC, A= 90 độ, B=30 độ AB= 8cm, Giải tam giác ABC bạn nhớ kẻ hình giúp tớ nhé
ΔABC vuông tại A
=>góc B+góc C=90 độ
=>góc C=60 độ
Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}\)
=>8/BC=căn 3/2
=>BC=16/căn 3(cm)
=>\(AC=\dfrac{8}{\sqrt{3}}\left(cm\right)\)
Đúng 0
Bình luận (0)
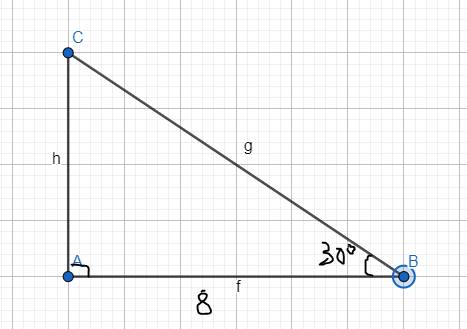
\(\widehat{C}=90^0-\widehat{B}=90^0-30^0=60^0\)
\(sin60=\dfrac{AB}{BC}=\dfrac{8}{BC}\Rightarrow BC=9,2\left(cm\right)\\ \sin30=\dfrac{AC}{BC}=\dfrac{AC}{9,2}\\ \Rightarrow AC=4,6\left(cm\right)\)
Đúng 1
Bình luận (0)