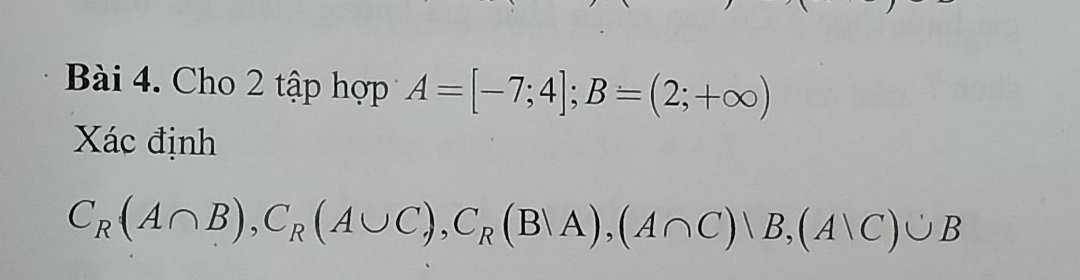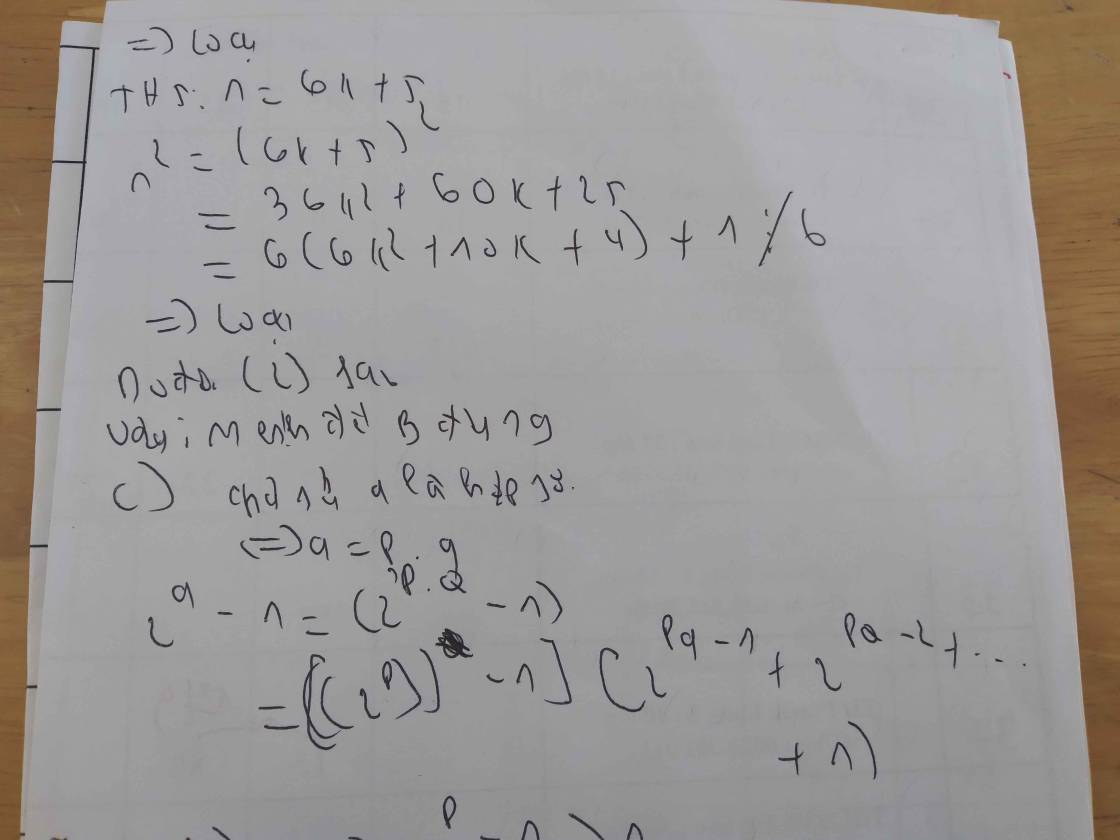Cho tam giác ABC có trung tuyến AM và I là trung điểm của AM. Chứng minh rằng: a) IB+IC= AM
§1. Mệnh đề
Ta có:
\(\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IM}\) (1)
Mặt khác: I là trung điểm AM
\(\Rightarrow\overrightarrow{AM}=2\overrightarrow{IM}\) (2)
Từ (1) và (2)
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{AM}\)
Đúng 1
Bình luận (0)
Cho ΔABC với các cạnh AB=c, BC=a. Gọi R,r,S lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác ABC. Trong các phát biểu sau, phát biểu nào sai ?
A. S=a.d.c/ 4R
B. R= a/ sin A
C. 1 phần 2.ab.sin C
D. a2 + b2 - c2 = 2ab. cos C
Trong các mệnh đề sau, mệnh đề nào đúng
A. 3 < √8
B. 3 > √8
C. 3 = √8
D. 3 ≤ 8
Ta có: \(3=\sqrt{3^2}=\sqrt{9}\)
Mà: \(9>8\)
\(\Rightarrow\sqrt{9}>\sqrt{8}\)
\(\Rightarrow3>\sqrt{8}\)
Vậy mệnh đề chính xác là B
Đúng 2
Bình luận (0)
giúp mình với ạ =)))
Câu 19: B
Câu 20: C
Câu 21: B
Câu 22: A
Câu 23: D
Câu 24: A
Câu 25: C
Câu 26: B
Câu 27: D
Câu 28: C
Câu 29: D
Đúng 0
Bình luận (0)
giúp mình với ạ mình có làm mà ko bt đúng hay ko, nhờ mn kiểm tra giùm=)))
Câu 11: D
Câu 12: D
Câu 13: C
Câu 14: B
Câu 15: C
Câu 16: C
Câu 18: C
Câu 17: A
Đúng 0
Bình luận (0)
giúp mình với ạ mình có làm mà ko bt đúng hay ko, nhờ mn kiểm tra giùm=)))
Câu 1: D
Câu 2: Những mệnh đề sai là: 2,3,4,5,7,8
=>Chọn B
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: D
Câu 7: D
Câu 8: C
Câu 9: D
Câu 10: B
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của x để mệnh đề P:"x2 + 5x + 4 = 0" là mệnh đề sai
\(x^2+5x+4=0\\ \Leftrightarrow x^2+x+4x+4=0\\ \Leftrightarrow x\left(x+1\right)+4\left(x+1\right)=0\\ \Leftrightarrow\left(x+4\right)\left(x+1\right)=0\\ \Leftrightarrow x+4=0.hoặc.x+1=0\\ \Leftrightarrow x=-4.hoặc.x=-1\\ Vậy.để.mệnh.đề.đó.là.mệnh.đề.sai:\\ \Leftrightarrow x\ne-4.hoặc.x\ne-1\)
Đúng 0
Bình luận (0)
lập mệnh đề phủ định của mệnh đề ∃x ∈R,x2+2x+5
Mệnh đề chưa đầy đủ. Bạn xem lại.
Đúng 0
Bình luận (0)
Đề bài không có tập C, bạn xem lại đề.
Đúng 0
Bình luận (0)
Xét tính Đ/S và c/m mệnh đề sau
A: '' nếu ∀ n ∈ N và n2 ⋮ 5 thì n⋮ 5 "
B: " ∀ x ∈ N và n2 ⋮ 6 thì n⋮ 6 "
C : '' nếu 2a - 1 là số nguyên tố thì a là số nguyên tố "
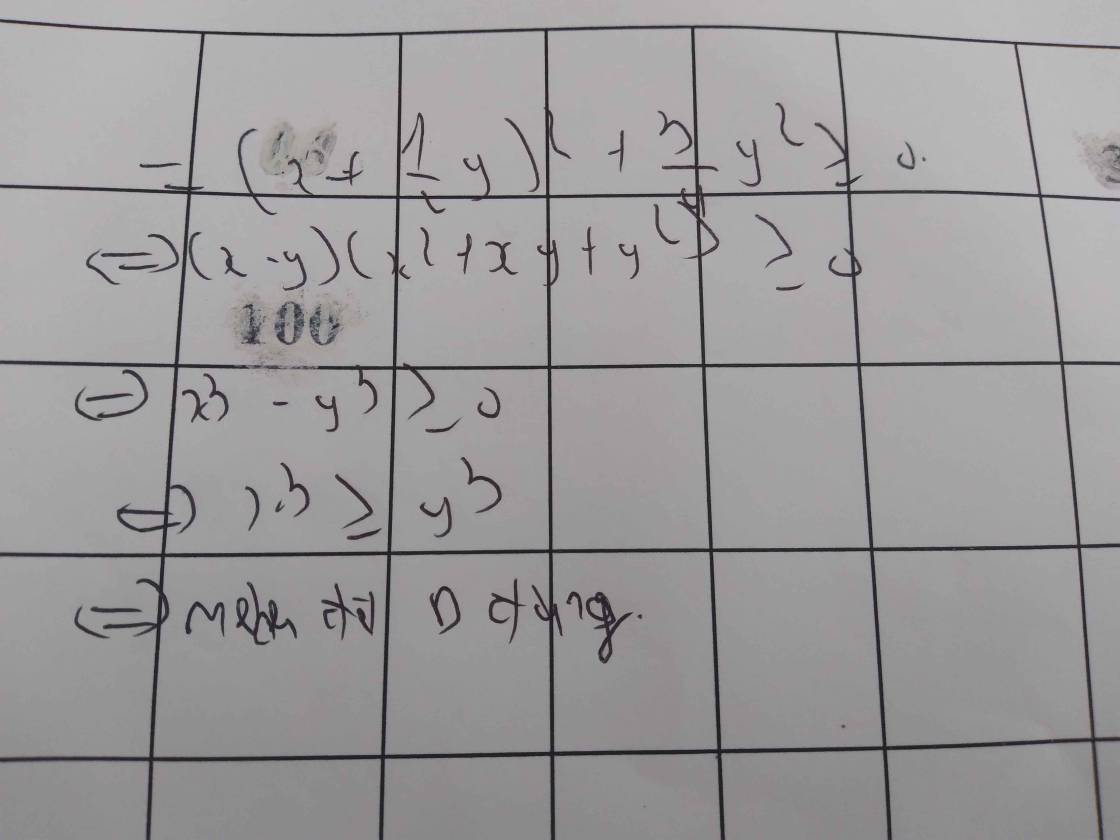
D: " nếu x≥y thì x3 ≥ y3 "