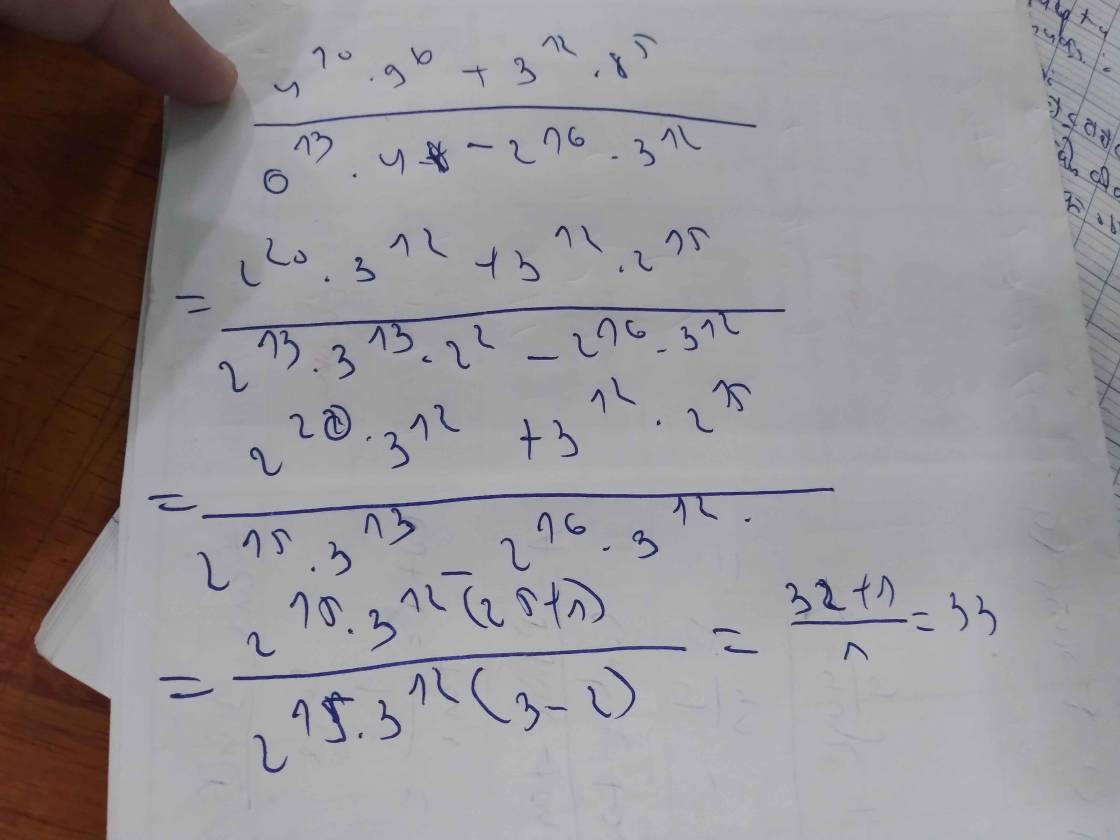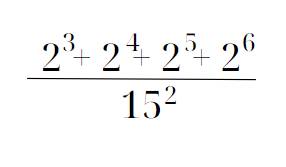6x3 - 3x2 + 2 /x/ + 4 với x = -2/3
Bài 5: Lũy thừa của một số hữu tỉ
`#3107.101107`
Thay `x = -2/3` vào biểu thức:
`6*(-2/3)^3 - 3*(-2/3)^2 + 2 * |-2/3| + 4`
`= 6 * (-8/27) - 3*4/9 + 2 * 2/3 + 4`
`= -16/9 - 4/3 + 4/3 + 4`
`= -16/9 + 4`
`= 20/9`
Vậy, giá trị của biểu thức là `20/9` tại `x = -2/3.`
Đúng 3
Bình luận (0)
410 . 96 + 312 . 85
______________
613 . 4 - 216 . 312
`#3107.101107`
\(\dfrac{4^{10}\cdot9^6+3^{12}\cdot8^5}{6^{13}\cdot4-2^{16}\cdot3^{12}}\)
\(=\dfrac{2^{20}\cdot3^{12}+3^{12}\cdot2^{15}}{2^{13}\cdot3^{13}\cdot2^2-2^{16}\cdot3^{12}}\)
\(=\dfrac{3^{12}\cdot\left(2^{20}+2^{15}\right)}{3^{12}\cdot\left(2^{15}\cdot3-2^{16}\right)}\)
\(=\dfrac{2^{20}+2^{15}}{2^{15}\cdot3-2^{16}}\)
\(=\dfrac{2^{15}\cdot\left(2^5+1\right)}{2^{15}\cdot\left(3-2\right)}\)
\(=\dfrac{32+1}{1}\)
\(=33\)
Đúng 2
Bình luận (0)
\(\dfrac{2^3+2^4+2^5+2^6}{15^2}\)
\(=\dfrac{2^3\cdot\left(1+2+2^2+2^3\right)}{15^2}\)
\(=\dfrac{8\cdot\left(1+2+4+8\right)}{15^2}\)
\(=\dfrac{8\cdot15}{15^2}\)
\(=\dfrac{8}{15}\)
Đúng 3
Bình luận (0)
\(\dfrac{2^3+2^4+2^5+2^6}{15^2}\)
\(=\dfrac{8+16+32+64}{225}\)
\(=\dfrac{120}{225}\)
\(=\dfrac{8}{15}\)
Đúng 3
Bình luận (0)
So sánh 6 mũ 8 và 16 mũ 12
\(6^8và16^{12}=\left(6.8\right)^0và\left(16.3\right)^9=48< 48^9\)
Đúng 0
Bình luận (0)
6⁸ = (6²)⁴ = 36⁴
16¹² = (16³)⁴ = 4096⁴
Do 36 < 4096 nên 36⁴ < 4096⁴
Vậy 6⁸ < 16¹²
Đúng 0
Bình luận (0)
Cách 2:
Do 6 < 16 nên 6¹² < 16¹² (1)
Do 8 < 12 nên 6⁸ < 6¹² (2)
Từ (1) và (2) ⇒ 6⁸ < 16¹²
Đúng 0
Bình luận (0)
(2²⁰.3²⁰ - 2²⁰.3¹⁹)/(2¹⁹.3²⁰)
= 2²⁰.3¹⁹.(3 - 1)/(2¹⁹.3²⁰)
= 2²⁰.3¹⁹.2/(2¹⁹.3²⁰)
= 2²¹.3¹⁹/(2¹⁹.3²⁰)
= 2²/3
= 4/3
Đúng 3
Bình luận (0)
\(\dfrac{2^{20}\cdot3^{20}-2^{20}\cdot3^{19}}{2^{19}\cdot3^{20}}\\ =\dfrac{2^{20}\cdot3^{19}\left(3-1\right)}{2^{19}\cdot3^{20}}\\ =\dfrac{2\cdot2}{3}\\ =\dfrac{4}{3}\)
Đúng 3
Bình luận (0)
16 ≤ 8ⁿ ≤64
⇒ 2⁴ ≤ (2³)ⁿ ≤ 2⁶
⇒ 4 ≤ 3n ≤ 6
⇒ 4/3 ≤ n ≤ 2
Do n là số nguyên dương nên n = 2
Đúng 2
Bình luận (0)
3³⁵ = (3⁷)⁵ = 2187⁵
5²⁰ = (5⁴)⁵ = 625⁵
Do 2187 > 625 nên 2187⁵ > 625⁵
Vậy 3³⁵ > 5²⁰
Đúng 1
Bình luận (0)
\(3^{35}và5^{20}=\left(3.5\right)^{30}và\left(5.3\right)^{17}=15^{30}>15^{17}\\ \Rightarrow3^{35}>5^{20}\)
Đúng 1
Bình luận (0)
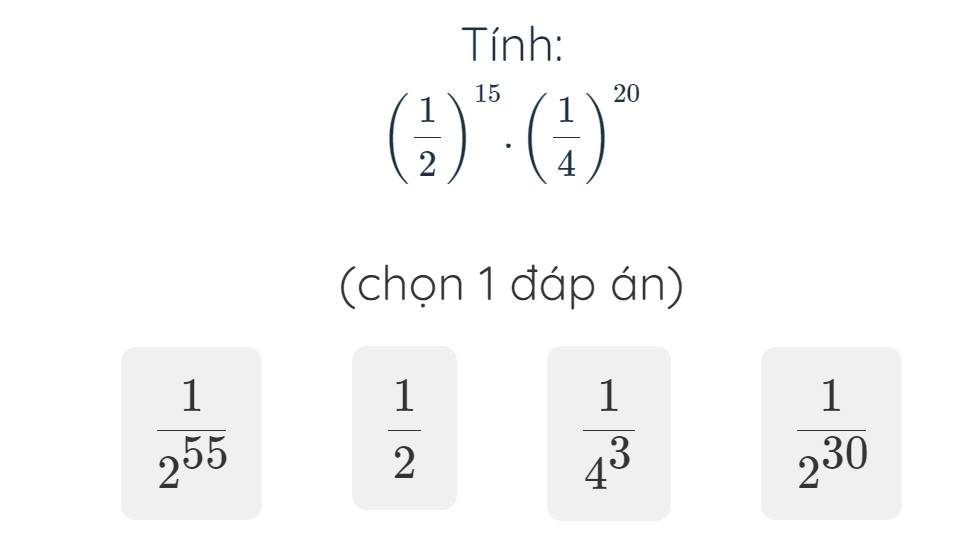
`(1/2)^15 * (1/4)^20`
`=(1/2)^15 * [(1/2)^2]^20`
`=(1/2)^15 * (1/2)^40`
`=(1/2)^55`
`=1/(2^55)`
Đúng 3
Bình luận (0)
bạn học vuihoc đúng ko
nhìn nó giống giao diện câu hỏi của vuihoc
Đúng 0
Bình luận (0)
Ta có: \(x^2+16\)
Mà: \(x^2\ge0\forall x\) nên:
\(\Rightarrow x^2+16\ge16\forall x\)
Dấu "=" xảy ra:
\(x^2+16=16\Leftrightarrow x=0\)
Vậy GTNN của biểu thức là 16 tại x=0
⇒ Chọn đáp án thứ nhất
Đúng 3
Bình luận (0)
\(F=\left(-\dfrac{1}{7}\right)^0+\left(-\dfrac{1}{7}\right)^1+...+\left(-\dfrac{1}{7}\right)^{2017}\)
=>\(7\cdot F=\left(-\dfrac{1}{7}\right)+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2018}\)
=>\(6\cdot F=\left(-\dfrac{1}{7}\right)^{2018}-1=\dfrac{1}{7^{2018}}-1=\dfrac{1-7^{2018}}{7^{2018}}\)
=>\(F=\dfrac{1-7^{2018}}{6\cdot7^{2018}}\)
Đúng 2
Bình luận (0)