chứng minh với x, y không âm ta có \(\dfrac{x+y}{2}\) ≥ \(\sqrt{xy}\)
Bài 2: Liên hệ giữa thứ tự và phép nhân
=>x+y>=2 căn xy
=>(căn x-căn y)^2>=0(luôn đúng)
Đúng 0
Bình luận (0)
A) cho a>b,b>0.Chứng minh a/b + b/a ≥2
B) cho a<b.Chứng minh; -2a - 3 > -2b - 3
C) chứng minh: x2 + 2y2 + 2xy + 6y +9 > 0
D) cho a + 3 > b + 3.Chứng minh: -5a + 1 < -5b +1
a: \(\dfrac{a}{b}+\dfrac{b}{a}>=2\cdot\sqrt{\dfrac{a}{b}\cdot\dfrac{b}{a}}=2\)
b: a<b
=>-2a>-2b
=>-2a-3>-2b-3
c: =x^2+2xy+y^2+y^2+6y+9
=(x+y)^2+(y+3)^2>=0 với mọi x,y
d: a+3>b+3
=>a>b
=>-5a<-5b
=>-5a+1<-5b+1
Đúng 1
Bình luận (0)
Cho ababab. Hãy so sánh 2a+342a+frac{3}{4}2a+43 và 2b+232b+frac{2}{3}2b+32?2a+34≤2b+232a+frac{3}{4}le2b+frac{2}{3}2a+43≤2b+32.2a+342b+232a+frac{3}{4} 2b+frac{2}{3}2a+432b+32.2a+
Đọc tiếp
Cho . Hãy so sánh và ?
..\(a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng).
-Dấu bằng xảy ra \(\Leftrightarrow a=b\)
Đúng 1
Bình luận (0)
Giúp e vs ạ , e chx hiểu lắm .
Đọc tiếp
Giúp e vs ạ , e chx hiểu lắm .
Bài 7:
a: a>b
nên -2a<-2b
=>-2a-6<-2b-6<-2b
b: a>b
nên 3a>3b
=>3a-9>3b-9
=>3(a-3)>3(b-3)
Đúng 1
Bình luận (0)
Giải phương trình sau:
a) | 2x-3 | - 4x - 9 = 0
b) (x + 1)2 - |5 - 3x| - x = x(x + 2) + 4
Em cảm ơn ạ
a: =>|2x-3|=4x+9
TH1: x>=3/2
=>4x+9=2x-3
=>2x=-12
=>x=-6(loại)
TH2: x<3/2
PT sẽ là 4x+9=3-2x
=>6x=-6
=>x=-1(nhận)
b: =>x^2+2x+1-|3x-5|-x-x^2-2x-4=0
=>-x-3-|3x-5|=0
=>x+3+|3x-5|=0
=>|3x-5|=-x-3
TH1: x>=5/3
Pt sẽ là 3x-5=-x-3
=>4x=2
=>x=1/2(loại)
TH2: x<5/3
Pt sẽ là 3x-5=x+3
=>2x=8
=>x=4(loại)
Đúng 0
Bình luận (0)
Giải dùm em từ câu 5 đến câu 12 với please 😭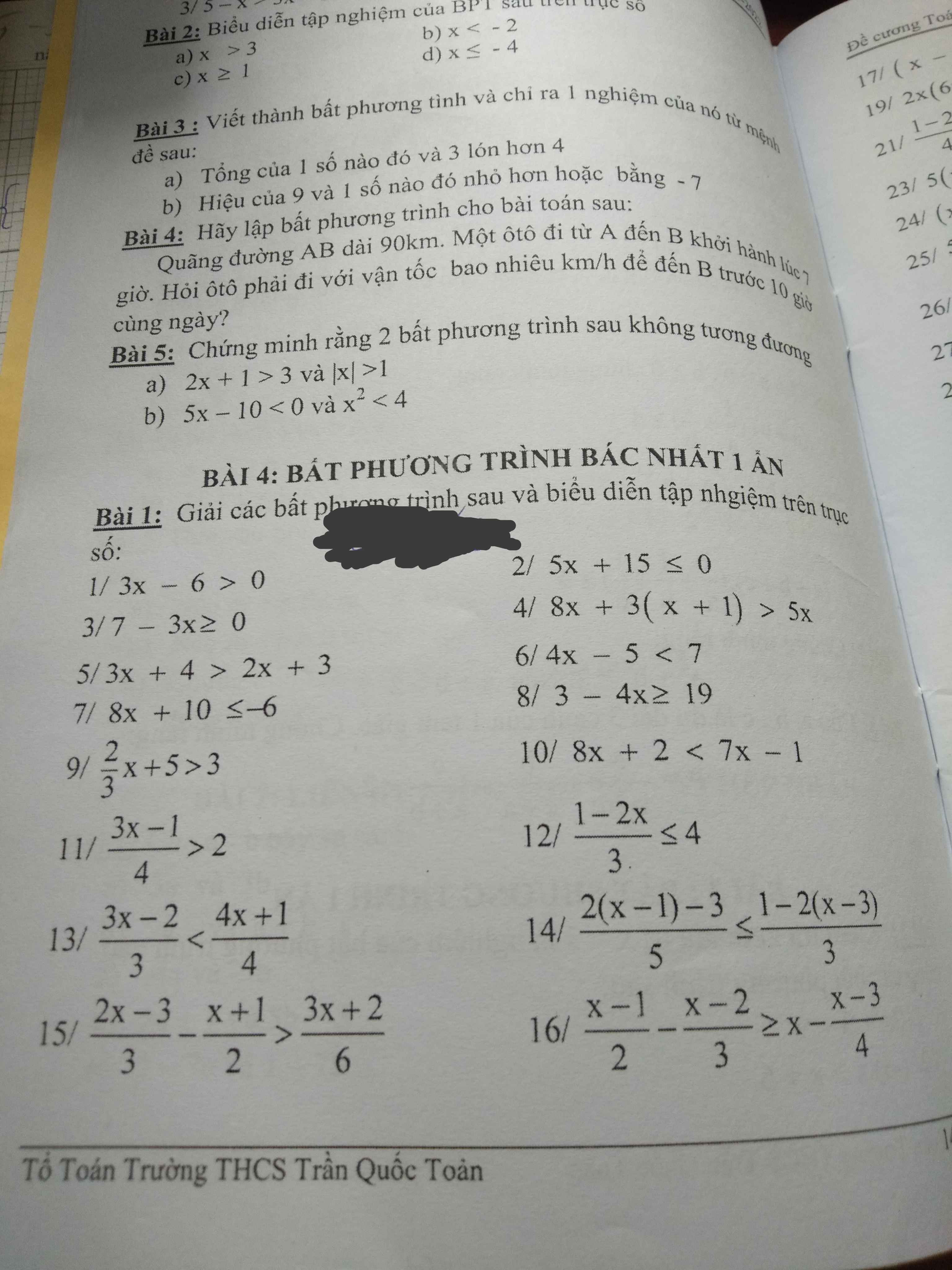
x^2+ 2x+3 > 0 đúng hay sai và tại sao?
\(x^2+2x+3=\left(x^2+2x+1\right)+2=\left(x+1\right)^2+1\ge1>0\)
Đúng 0
Bình luận (0)
cho m<n, cmr
a,-3n+2<-3m+2
b,5m-3<5n+7
a)-3n+2<-3m+2
⇒-3n<-3m
⇒3n>3m
⇒n>m
b)5m-3<5n+7
⇔5m<5n+10
⇔m<n+2
Đúng 0
Bình luận (0)
2x/x-1-x/x+1=1
đk : x khác -1 ; 1
\(2x^2+2x-x^2+x=x^2-1\Leftrightarrow3x=-1\Leftrightarrow x=-\dfrac{1}{3}\left(tm\right)\)
Đúng 1
Bình luận (1)


















