Cho hình vẽ biết DE//BC.
a, Viết cặp tam giác đồng dạng và tính tỉ số đồng dạng của tam giác đó.
b, Tính các góc của tam giác ADE.
c, Tính AD.
Cho hình vẽ biết DE//BC.
a, Viết cặp tam giác đồng dạng và tính tỉ số đồng dạng của tam giác đó.
b, Tính các góc của tam giác ADE.
c, Tính AD.
bạn cho mình xin hình vẽ nha bạn
chu vi của △ABC.Tính chu vi của mỗi tam giác biết tổng chu vi của hai tam giác là 63cm
https://hoc24.vn/cau-hoi/cho-abcgoi-de-la-hai-diem-lan-luot-thuoc-ab-va-ac-sao-cho-debc-xac-dinh-vi-tri-cua-diem-d-de-chu-vi-cua-ade-dfrac25-chu-vi-cua-abctinh-chu-vi-cua-moi-tam-giac-biet-tong-chu-vi-cua.8813432327782#:~:text=Cho%C2%A0%E2%96%B3ABC.G%E1%BB%8Di,gi%C3%A1c%20l%C3%A0%2063cm
cho tam giác MNP vuông tại M MN = 6 cm MP = 8 cm NP = 10 cm đồng dạng với tam giác ABC tam giác ABC có cạnh nhỏ nhất là 3cm.Tính các cạnh còn lại
ΔMNP~ΔABC
=>\(\dfrac{MN}{AB}=\dfrac{NP}{BC}=\dfrac{MP}{AC}\)
=>\(\dfrac{6}{3}=\dfrac{10}{BC}=\dfrac{8}{AC}\)
=>\(\dfrac{10}{BC}=\dfrac{8}{AC}=2\)
=>\(BC=10:2=5\left(cm\right);AC=8:2=4\left(cm\right)\)
Cho △ABC.Gọi D,E là hai điểm lần lượt thuộc AB và AC sao cho DE//BC. Xác định vị trí của điểm D để chu vi của △ADE = \(\dfrac{2}{5}\) chu vi của △ABC.Tính chu vi của mỗi tam giác biết tổng chu vi của hai tam giác là 63cm
Cho ABC. Gọi D và E là hai điểm lần lượt thuộc AB và AC sao cho DE//BC. Xác định vị trí của điểm D để chu vi của tam giác ADE bằng chu vi của tam giác ABC. Tính chu vi của mỗi tam giác biết tổng chu vi của hai tam giác là 63 cm
Cho △ ABC.Từ điểm A kẻ tia Am//BC.Gọi D là trung điểm của BC.Qua D kẻ đường thẳng bất kì cắt AM tại E,cắt AC tại Q và cắt AB tại P.CMR \(\dfrac{PE}{PD}\) = \(\dfrac{QE}{QD}\)
Bài này của em hình như giống hệt bài trước, khác đúng 1 chi tiết về tỉ lệ \(\dfrac{OA}{OD}=\dfrac{3}{2}\)
Đồng nghĩa với việc chỗ nào có 2/3 ở bài trước em đổi thành 3/2 là lời giải ko khác nhau dù chỉ 1 chữ.
a.
Do AB song song DE, áp dụng định lý Talet:
\(\dfrac{AB}{DE}=\dfrac{OA}{OD}=\dfrac{2}{3}=\dfrac{OB}{OE}\) (1)
Do AC song song DF, áp dụng định lý Talet:
\(\dfrac{AC}{DF}=\dfrac{OA}{OD}=\dfrac{2}{3}=\dfrac{OC}{OF}\) (2)
(1);(2) \(\Rightarrow\dfrac{OB}{OE}=\dfrac{OC}{OF}\Rightarrow BC||EF\) (Talet đảo)
\(\Rightarrow\dfrac{BC}{EF}=\dfrac{OB}{OE}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}\Rightarrow\Delta ABC\sim\Delta DEF\left(c.c.c\right)\)
b.
Ta có: \(\left\{{}\begin{matrix}\dfrac{AB}{DE}=\dfrac{2}{3}\\DE-AB=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{2}{3}DE\\DE-\dfrac{2}{3}DE=12\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}DE=36\\AB=\dfrac{2}{3}.36=24\end{matrix}\right.\)
c.
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{2}{3}=\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}=\dfrac{AB+AC+BC}{DE+DF+EF}\)
\(\Rightarrow AB+AC+BC=\dfrac{2}{3}\left(DE+DF+EF\right)\)
Mà \(\left(DE+DF+EF\right)+\left(AB+AC+BC\right)=120\)
\(\Rightarrow\left(DE+DF+EF\right)+\dfrac{2}{3}\left(DE+DF+EF\right)=120\)
\(\Rightarrow\dfrac{5}{3}\left(DE+DF+EF\right)=120\)
\(\Rightarrow DE+DF+EF=72\)
cho tam giác ABC nhọn. Trên tia đối của tia BA lấy điểm D sao cho 2BD=BA. Trên tia đối của tia CA lấy điểm E sao cho 2CE=CA. Chứng minh tam giác ABC đồng dạng với tam giác ADE
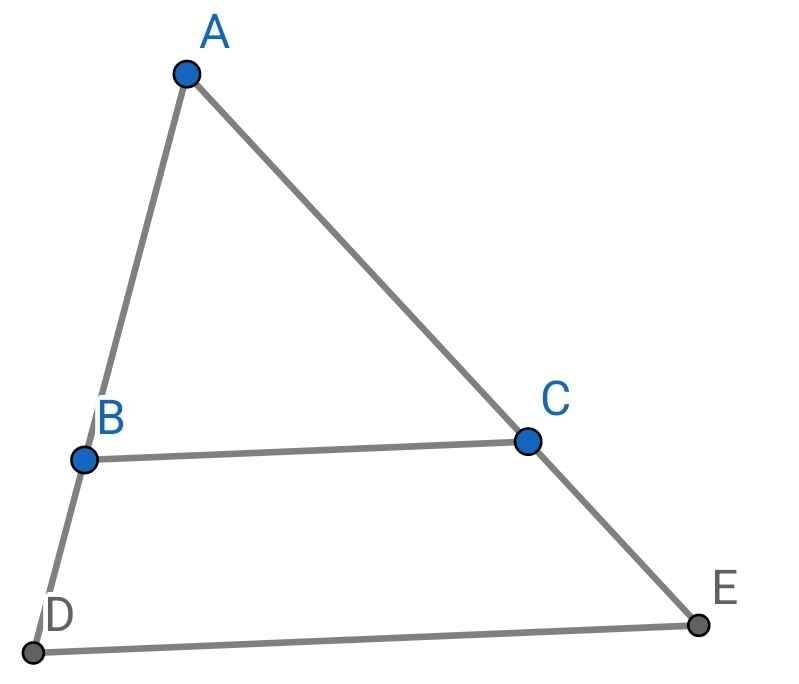 Do 2BD = BA (gt)
Do 2BD = BA (gt)
⇒ AD = AB + BD
= 2BD + BD
= 3BD
⇒ AB/AD = 2/3 (1)
Do 2CE = CA (gt)
⇒ AE = AC + CE
= 2CE + CE
= 3CE
⇒ AC/AE = 2/3 (2)
Từ (1) và (2) ⇒ AB/AD = AC/AE = 2/3
Xét ∆ABC và ∆ADE có:
AB/AD = AC/AE (cmt)
A chung
⇒ ∆ABC ∽ ∆ADE (c-g-c)