Bài 1: Định lý Talet trong tam giác

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=6^2+8^2=100=10^2\)

=>BC=10(cm)

Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{6}=\dfrac{DC}{8}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

mà DB+DC=BC=10cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)

=>\(DB=3\cdot\dfrac{10}{7}=\dfrac{30}{7}\left(cm\right);DC=4\cdot\dfrac{10}{7}=\dfrac{40}{7}\left(cm\right)\)

b: 

Kẻ DH\(\perp\)AC

=>DH là khoảng cách từ D đến AC

DH\(\perp\)AC

AB\(\perp\)AC

Do đó: DH//AB

Xét ΔCAB có DH//AB

nên \(\dfrac{DH}{AB}=\dfrac{CD}{CB}\)

=>\(\dfrac{DH}{6}=\dfrac{40}{7}:10=\dfrac{4}{7}\)

=>\(DH=\dfrac{24}{7}\)(cm)

c: Xét ΔABC có AD là phân giác

nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)

\(=\dfrac{2\cdot6\cdot8}{6+8}\cdot cos45\)

\(=\dfrac{24\sqrt{2}}{7}\left(cm\right)\)

a: Xét ΔEDA và ΔEGC có

\(\widehat{EDA}=\widehat{EGC}\)(hai góc so le trong, AD//CG)

\(\widehat{DEA}=\widehat{GEC}\)(hai góc đối đỉnh)

Do đó: ΔEDA~ΔEGC

=>\(\dfrac{ED}{EG}=\dfrac{EA}{EC}\left(1\right)\)

Xét ΔABC có DE//BC

nên \(\dfrac{EA}{EC}=\dfrac{AD}{DB}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{ED}{EG}=\dfrac{AD}{DB}\)

=>\(ED\cdot DB=EG\cdot AD\)

b: Xét ΔHEG và ΔHCB có

\(\widehat{HEG}=\widehat{HCB}\)(hai góc so le trong, EG//BC)

\(\widehat{EHG}=\widehat{CHB}\)(hai góc đối đỉnh)

Do đó: ΔHEG~ΔHCB

=>\(\dfrac{HE}{HC}=\dfrac{EG}{CB}\)(3)

Xét ΔHGC và ΔHBA có

\(\widehat{HGC}=\widehat{HBA}\)(hai góc so le trong, AB//CG)

\(\widehat{GHC}=\widehat{BHA}\)(hai góc đối đỉnh)

Do đó: ΔHGC~ΔHBA

=>\(\dfrac{HC}{HA}=\dfrac{GC}{BA}\left(4\right)\)

Xét tứ giác BDGC có

BD//GC

DG//BC

Do đó:BDGC là hình bình hành

=>\(\widehat{DGC}=\widehat{DBC}\)

Xét ΔGEC và ΔBCA có

\(\widehat{GEC}=\widehat{BCA}\)(hai góc so le trong, EG//BC)

\(\widehat{EGC}=\widehat{CBA}\)(cmt)

Do đó: ΔGEC~ΔBCA

=>\(\dfrac{EG}{BC}=\dfrac{GC}{BA}\left(5\right)\)

Từ (3),(4),(5) suy ra \(\dfrac{HC}{HA}=\dfrac{HE}{HC}\)

=>\(HC^2=HE\cdot HA\)

a: Ta có: BE\(\perp\)DC

AC\(\perp\)DC

Do đó: BE//AC

Xét ΔDAC có ME//AC

nên \(\dfrac{DM}{DA}=\dfrac{DE}{DC}\)

b: Ta có: NE\(\perp\)BD

BC\(\perp\)BD

Do đó: NE//BC

Xét ΔDBC có NE//BC

nên \(\dfrac{DE}{DC}=\dfrac{DN}{DB}\)

=>\(\dfrac{DN}{DB}=\dfrac{DM}{DA}\)

Xét ΔDBA có \(\dfrac{DN}{DB}=\dfrac{DM}{DA}\)

nên MN//AB

Ta có:

\(\dfrac{AB}{AD}=\dfrac{6}{4}=\dfrac{3}{2}\)

\(\dfrac{AC}{AE}=\dfrac{9}{6}=\dfrac{3}{2}\)

\(\Rightarrow\dfrac{AB}{AD}=\dfrac{AC}{AE}=\dfrac{3}{2}\)

Xét 2 tam giác ABC và tam giác ADE ta có: 

\(\widehat{CAB}\) chung 

\(\dfrac{AB}{AD}=\dfrac{AC}{AE}\left(=\dfrac{3}{2}\right)\) 

\(\Rightarrow\Delta ABC\sim\Delta ADE\left(c.g.c\right)\)

\(\Rightarrow\dfrac{DE}{BC}=\dfrac{AB}{AD}=\dfrac{AC}{AE}=\dfrac{3}{2}\)

Vậy: ... 

Bài 8:

a: Xét ΔBAC có EF//BC

nên \(\dfrac{BE}{EA}=\dfrac{BF}{FC}\)

=>\(\dfrac{BF}{FC}=2\)

=>\(\dfrac{CF}{FB}=\dfrac{1}{2}\)

Xét ΔCDB có GF//BD

nên \(\dfrac{CF}{FB}=\dfrac{CG}{GD}\)

=>\(\dfrac{CG}{GD}=\dfrac{1}{2}\)

=>\(\dfrac{DG}{CG}=2\)

Xét ΔDAC có GH//AC

nên \(\dfrac{DH}{AH}=\dfrac{DG}{CG}=2\)

=>\(\dfrac{AH}{DH}=\dfrac{1}{2}\)

b: Xét ΔABD có \(\dfrac{AE}{EB}=\dfrac{AH}{HD}\)

nên EH//BD

c: Ta có: EH//BD

GF//BD

Do đó: EH//GF

Ta có: EF//AC

GH//AC

Do đó: EF//GH

Xét tứ giác EFGH có

EF//GH

EH//GF

Do đó: EFGH là hình bình hành

11:

Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB đồng dạng với ΔOCD

=>\(\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{12}{30}=\dfrac{2}{5}\)

=>\(\dfrac{OB}{2}=\dfrac{OD}{5}\)

mà OB+OD=BD=21

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{OB}{2}=\dfrac{OD}{5}=\dfrac{OB+OD}{2+5}=\dfrac{21}{7}=3\)

=>\(OB=2\cdot3=6\left(cm\right);OD=3\cdot5=15\left(cm\right)\)

Bài 12:

Xét ΔABC có DE//BC

nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}\)

=>\(\dfrac{AD}{AD+DB}=\dfrac{4}{10}=\dfrac{2}{5}\)

=>\(\dfrac{AD}{AD+3}=\dfrac{2}{5}\)

=>\(5\cdot AD=2\left(AD+3\right)\)

=>\(5\cdot AD-2\cdot AD=2\cdot3\)

=>\(3\cdot AD=6\)

=>AD=2(cm)

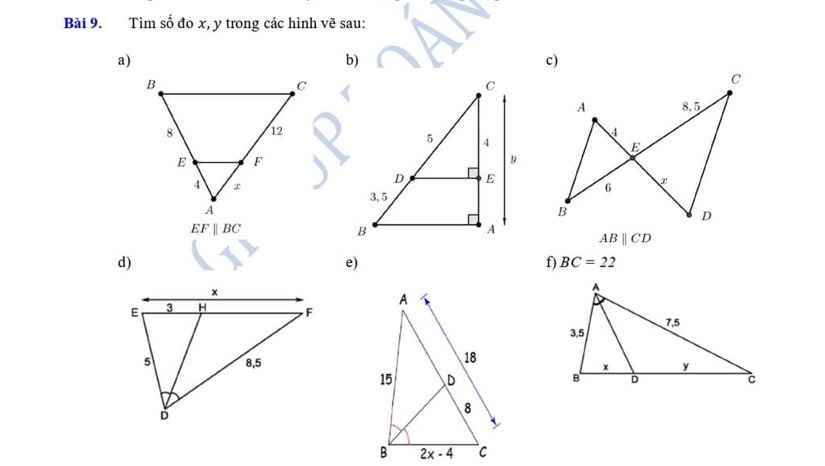
a: Xét ΔABC có EF//BC

nên \(\dfrac{AF}{FC}=\dfrac{AE}{EB}\)

=>\(\dfrac{x}{12}=\dfrac{4}{8}=\dfrac{1}{2}\)

=>x=12/2=2=6

b: CB=CD+DB

=5+3,5

=8,5

Xét ΔCAB có DE//AB

nên \(\dfrac{CE}{CA}=\dfrac{CD}{CB}\)

=>\(\dfrac{4}{y}=\dfrac{5}{8,5}\)

=>\(y=\dfrac{4\cdot8,5}{5}=\dfrac{34}{5}=6,8\)

c: Xét ΔEAB và ΔEDC có

\(\widehat{EAB}=\widehat{EDC}\)(hai góc so le trong, AB//DC)

\(\widehat{AEB}=\widehat{DEC}\)(hai góc đối đỉnh)

Do đó: ΔEAB đồng dạng với ΔEDC

=>\(\dfrac{EA}{ED}=\dfrac{EB}{EC}\)

=>\(\dfrac{4}{x}=\dfrac{6}{8,5}\)

=>\(x=4\cdot\dfrac{8.5}{6}=\dfrac{17}{3}\)

d: Xét ΔDEF có DH là phân giác

nên \(\dfrac{HE}{ED}=\dfrac{HF}{FD}\)

=>\(\dfrac{HF}{8,5}=\dfrac{3}{5}\)

=>HF=8,5*3/5=5,1

x=EF=EH+HF=3+5,1=8,1

e:
DC+DA=AC

=>DA+8=18

=>DA=10

Xét ΔBCA có BD là phân giác

nên \(\dfrac{BC}{CD}=\dfrac{BA}{AD}\)

=>\(\dfrac{BC}{BA}=\dfrac{CD}{AD}\)

=>\(\dfrac{BC+BA}{BA}=\dfrac{CD+AD}{AD}\)
=>\(\dfrac{2x-4+15}{15}=\dfrac{18}{10}=\dfrac{9}{5}\)

=>\(2x+11=\dfrac{9}{5}\cdot15=9\cdot3=27\)

=>2x=16

=>x=8

f: Xét ΔABC có AD là phân giác

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)

=>\(\dfrac{x}{3,5}=\dfrac{y}{7,5}\)

mà x+y=BC=22

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{3,5}=\dfrac{y}{7,5}=\dfrac{x+y}{3,5+7,5}=\dfrac{22}{11}=2\)

=>\(x=2\cdot3,5=7;y=2\cdot7,5=15\)

1: Xét tứ giác AECF có

M là trung điểm chung của AC và EF

=>AECF là hình bình hành

2:

Ta có: ΔHAC vuông tại H

mà HM là đường trung tuyến

nên HM=AC/2

Xét ΔMAH và ΔMKF có

\(\widehat{MAH}=\widehat{MFK}\)(hai góc so le trong, AH//FK)

\(\widehat{AMH}=\widehat{KMF}\)

Do đó: ΔMAH đồng dạng với ΔMKF

=>\(\dfrac{AH}{KA}=\dfrac{MH}{MF}=\dfrac{\dfrac{1}{2}AC}{\dfrac{1}{2}FE}=\dfrac{AC}{FE}\)

Bổ sung đề: Kẻ DF vuông góc với AB

a: Xét tứ giác AEDF có

\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)

=>AEDF là hình chữ nhật

b: Ta có: AEDF là hình chữ nhật

=>O là trung điểm chung của AD và EF và AD=EF(1)

O là trung điểm của AD

nên \(OA=DO=\dfrac{AD}{2}\left(2\right)\)

O là trung điểm của EF

=>\(OE=OF=\dfrac{FE}{2}\left(3\right)\)

Từ (1),(2),(3) suy ra OA=DO=OE=OF=EF/2=AD/2

Ta có: ΔHAD vuông tại H

mà HO là đường trung tuyến

nên \(HO=\dfrac{1}{2}AD=\dfrac{1}{2}\cdot EF\)

c:

Ta có; ΔAHD vuông tại H

=>AD là cạnh huyền

=>AH<=AD

Để EF nhỏ nhất thì AD nhỏ nhất

mà AH<=AD

Dấu '=' xảy ra khi H trùng với D

Vậy: D là chân đường cao kẻ từ A xuống BC

Bạn không hiểu bước nào thì cứ hỏi nha

Bn nguyên lê phước  thịnh ơi bn trl giúp mik đc ko MIK KO HIỂU DÒNG 2 Á