Cho tam giác đều ABC có cạnh bằng 4cm. M, N là các điểm lần lượt chuyển động trên hai cạnh BC và AC sao cho BM = CN.
a) Tính diện tích của tam giác ABC.
b) Xác định vị trí của M, N để độ dài đoạn thẳng MN nhỏ nhất. Tìm độ dài nhỏ nhất đó.
Cho tam giác đều ABC có cạnh bằng 4cm. M, N là các điểm lần lượt chuyển động trên hai cạnh BC và AC sao cho BM = CN.
a) Tính diện tích của tam giác ABC.
b) Xác định vị trí của M, N để độ dài đoạn thẳng MN nhỏ nhất. Tìm độ dài nhỏ nhất đó.
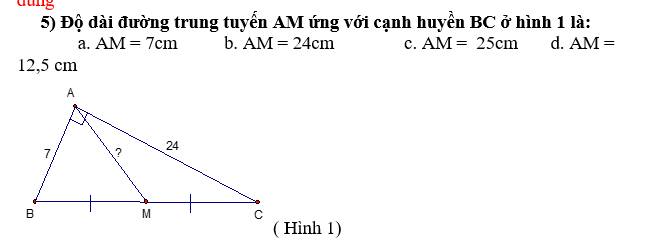
giúp mình với đang cần gấp để thi
câu D
áp dụng dl pytago có sẽ tính được bc=25
trung tuyến ứng với cạnh huyền bằng nữa cạnh huyền 25/2=12,5
cho tam giác ABC vuông tại A, tính độ dài cạnh BC trong trường hợp sau : AB = 2AC và AB + AC
cho tam giác ABC nhọn, góc BAC= 70 độ kẻ BK vuông góc với AC tại K và CI vuông góc với AB tại I Gọi H là giao điểm BC và CI a) CMR: AH vuông góc BC b) Tính góc BHC
a: Xét ΔABC có
BK,CI là đường cao
BK cắt CI tại H
=>H là trực tâm
=>AH vuông góc BC
b: góc HBC+góc HCB
=90 độ-góc ABC+90 độ-góc ACB
=180 độ-góc ABC-góc ACB
=góc BAC=70 độ
=>góc BHC=110 độ
Cho tam giác ABC vuông tại A (AB<AC) có đường cao AH, biết AB=12cm, AC=16cm
a) Tính BC và AH
b) Chứng minh tam giác BHA đồng dạng tam giác ABC
a: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=192/20=9,6cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
Tính tỉ số của chu vi hình tam giác biết cạnh thứ nhất bằng 6cm, cạnh thứ hai bằng 7,5cm
A. 2/3
B. 3/2
C. 1/2
D. 2
Một hình tam giác có một cạnh là 5cm và một cạnh 7,5cm. Tính độ dài cạnh còn lại?
Gọi độ dài cạnh còn lại là a
Theo đề, ta có: 7,5-5<a<7,5+5
=>2,5<a<12,5
Cho∆ ABC vuông tại A có BA=6cm và BC=10cm và BD cắt AC cho AD là x và DC là y tính độ dài x,y
\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5
=>x/3=y/5=(x+y)/(3+5)=8/8=1
=>x=3
y=5
Cho tam giác ABC có chu vi là 10 cm, giao điểm I của các đường phân giác các cạnh 1 cm. Tính diện tích tam giác ABC
Cho hình thang abcd ab//CD o là giao đ 2 đag chéo
Cm Soad=12 cm^2 Sobc=27 cm^2
tinhs Sabcd