rút gọn biểu thức A= ∛2 + √7+2√10 + ∛3∛4 - 3∛2 -1
Bài 9: Căn bậc ba
Chứng minh rằng biểu thức \(\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}}\le2\) với mọi số thực \(x\) (\(x\ge0\))
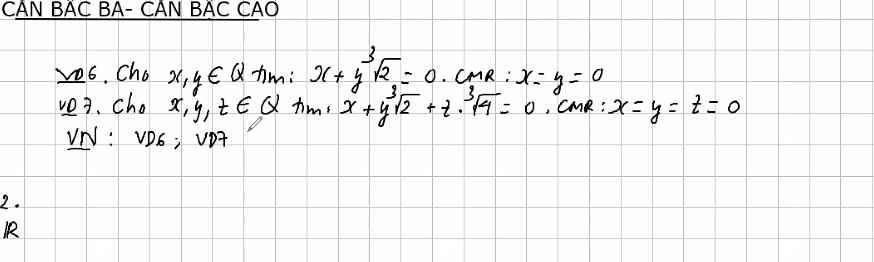 Nhờ mọi người giúp nình với ạ
Nhờ mọi người giúp nình với ạ
\(\sqrt[3]{x+1}+\sqrt[3]{x+8}=\sqrt[3]{2x+27}\)
\(\sqrt[3]{x+1}+\sqrt[3]{x+8}=\sqrt[3]{2x+27}\)
cho các số dương x+y+z=2012 . cmr x^2/y^z + y^2/x+z + z^2/x+y >= 2016
Tính: \(\dfrac{2}{\sqrt[3]{3}-1}-\dfrac{4}{\sqrt[3]{9}-\sqrt[3]{3}+1}\)
giúp em với tính giá trị biểu thức
\(A=\dfrac{2}{\sqrt[4]{7}}-\sqrt[4]{7}-\dfrac{\sqrt{7}-\dfrac{1}{\sqrt{7}}}{\sqrt[4]{7}-\sqrt{\dfrac{1}{\sqrt{7}}}}+\dfrac{6}{\sqrt{7}\left(\sqrt[4]{7+\sqrt[4]{\dfrac{1}{7}}}\right)}+\dfrac{7}{\sqrt[4]{343}}\)
Gọi vận tốc lúc đầu là x (km/h)- vận tốc lúc sau là x+ 6 (km/h)Thời gian bạn Hà đi lúc đầu là dfrac{120}{x} (h)Một giờ bạn Hà đi được S t.v x.1 x (km)Thời bạn Hà đi sau khi tăng tốc là dfrac{120-x}{x+6} (h)Đổi 10 phút dfrac{1}{6} giờTheo đề bài ta được phương trình:dfrac{120}{x} dfrac{120-x}{x+6}+1+dfrac{1}{6}
Đọc tiếp
Gọi vận tốc lúc đầu là x (km/h)
-> vận tốc lúc sau là x+ 6 (km/h)
Thời gian bạn Hà đi lúc đầu là \(\dfrac{120}{x}\) (h)
Một giờ bạn Hà đi được S = t.v = x.1 = x (km)
Thời bạn Hà đi sau khi tăng tốc là \(\dfrac{120-x}{x+6}\) (h)
Đổi 10 phút = \(\dfrac{1}{6}\) giờ
Theo đề bài ta được phương trình:
\(\dfrac{120}{x}\) = \(\dfrac{120-x}{x+6}+1+\dfrac{1}{6}\)
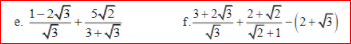
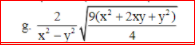
Rút gọn biểu thức












