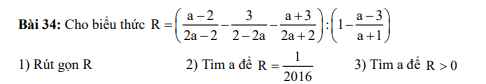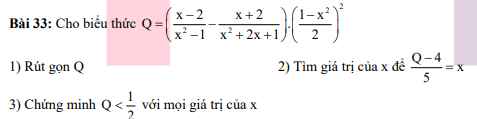Bài 3: Bất phương trình một ẩn

Gọi qđ AB lúc đi là x(km) x>0

Thời gian từ A đến B lúc đi là \(\dfrac{x}{30}\) (h)

Qđ AB lúc về là : x+15

Thời gian lúc về là \(\dfrac{x+15}{40}\) (h)

Theo bài ra ta có pt

\(\dfrac{x}{30}\)-\(\dfrac{x+15}{40}\)=\(\dfrac{30}{60}\)

Giải ra được x=105(km)

Vậy...

Gọi độ dài quãng đường AB là x

Thời gian đi là x/50(h)

Thời gian về là x/40(h)

Theo đề, ta có: x/50+x/40=2,25

hay x=50

Gọi quãng đường AB là x(m) (x<0)
Thời gan ô tô đi từ A đến B là
Thời gian ô tô đi từ B về A là x/40
Đổi 2h15p=2,25 (h)
Theo bài ra ta có phương trình:
 x/50+x/40=2,25
⟺40x/200+50x/200=2,25
⟺90x=2,25
⟺x=90/2,25=50 ( thõa mãn)
Vậy quãng đường AB dài 50km

giúp mik đi ạ đang gấp

x+1<x+2<x+3<x+4 ( với mọi x)

\(\dfrac{1}{100}\) < \(\dfrac{1}{99}\)<\(\dfrac{1}{3}\) <\(\dfrac{1}{2}\)

=>\(\dfrac{x+1}{100}\)+\(\dfrac{x+2}{99}\) <\(\dfrac{x+3}{3}\)+\(\dfrac{x+4}{2}\) là đúng

\(\Leftrightarrow3\left(1-2x\right)-2\left(x+1\right)< =6\)

=>3-6x-2x-2<=6

=>-8x+1<=6

=>-8x<=5

hay x>=5/8

1.

ĐK: \(a\ne\pm1\)

\(R=\left(\dfrac{a-2}{2a-2}-\dfrac{3}{2-2a}-\dfrac{a+3}{2a+2}\right):\left(1-\dfrac{a-3}{a+1}\right)\)

\(=\left[\dfrac{a+1}{2\left(a-1\right)}-\dfrac{a+3}{2\left(a+1\right)}\right]:\left(1-\dfrac{a-3}{a+1}\right)\)

\(=\left[\dfrac{\left(a+1\right)^2-\left(a+3\right)\left(a-1\right)}{2\left(a-1\right)\left(a+1\right)}\right]:\left(\dfrac{a+1-a+3}{a+1}\right)\)

\(=\left[\dfrac{a^2+2a+1-a^2-2a+3}{2\left(a-1\right)\left(a+1\right)}\right]:\dfrac{4}{a+1}\)

\(=\dfrac{4}{2\left(a-1\right)\left(a+1\right)}.\dfrac{a+1}{4}\)

\(=\dfrac{1}{2a-2}\)

2.

\(R=\dfrac{1}{2016}\Leftrightarrow\dfrac{1}{2a-2}=\dfrac{1}{2016}\)

\(\Leftrightarrow2a-2=2016\)

\(\Leftrightarrow a=1009\)

3.

\(R>0\Leftrightarrow\dfrac{1}{2a-2}>0\)

\(\Leftrightarrow2a-2>0\)

\(\Leftrightarrow a>1\)

1: \(Q=\dfrac{x^2-x-2-x^2-x+2}{\left(x+1\right)^2\left(x-1\right)}\cdot\dfrac{\left(x-1\right)^2\left(x+1\right)}{4}\)

\(=\dfrac{-2x\left(x-1\right)}{\left(x+1\right)4}=\dfrac{-x\left(x-1\right)}{2\left(x+1\right)}\)

a: ĐKXĐ: \(a\notin\left\{0;-5\right\}\)

Lời giải:

Gọi biểu thức đã cho là $A$.

CM vế 1:

Ta có:

$\frac{a+b}{a+b+c}> \frac{a+b}{a+b+c+d}$

$\frac{b+c}{b+c+d}> \frac{b+c}{a+b+c+d}$

$\frac{c+d}{c+d+a}> \frac{c+d}{a+b+c+d}$

$\frac{d+a}{d+a+b}> \frac{d+a}{a+b+c+d}$

Cộng lại: $A> \frac{2(a+b+c+d)}{a+b+c+d}=2>1$

CM vế 2:

Ta thấy $\frac{a+b}{a+b+c}-\frac{a+b+d}{a+b+c+d}=\frac{-cd}{(a+b+c)(a+b+c+d)}< 0$ với $a,b,c,d>0$

$\Rightarrow \frac{a+b}{a+b+c}< \frac{a+b+d}{a+b+c+d}$

Hoàn toàn tương tự với các phân thức còn lại:

$\Rightarrow A< \frac{3(a+b+c+d)}{a+b+c+d}=3$

Ta có đpcm.