Giải các pt mũ sau:
a) \(16^{-x} = 8^{2(1-x)}\)
b) \(3^{|3x-4|}= 9^{2x-2}\)
c) \(32^{\frac{x+5}{x-4}} = 0,25. 128^{\frac{x+17}{x-3}}\)
d) \(6^x . 2^{-x}.3^{x+1}= 3^{x-1}\)
Giải các pt mũ sau:
a) \(16^{-x} = 8^{2(1-x)}\)
b) \(3^{|3x-4|}= 9^{2x-2}\)
c) \(32^{\frac{x+5}{x-4}} = 0,25. 128^{\frac{x+17}{x-3}}\)
d) \(6^x . 2^{-x}.3^{x+1}= 3^{x-1}\)
a: \(16^{-x}=8^{2\left(1-x\right)}\)
=>\(2^{-4x}=2^{6\left(1-x\right)}\)
=>6(1-x)=-4x
=>6-6x=-4x
=>-4x+6x=6
=>2x=6
=>x=6/2=3
b: \(3^{\left|3x-4\right|}=9^{2x-2}\)
=>\(3^{\left|3x-4\right|}=3^{4x-4}\)
=>\(\left|3x-4\right|=4x-4\)
=>\(\left\{{}\begin{matrix}4x-4>=0\\\left(4x-4\right)^2=\left(3x-4\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=1\\\left(4x-4-3x+4\right)\left(4x-4+3x-4\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=1\\x\left(7x-8\right)=0\end{matrix}\right.\)
=>\(x=\dfrac{8}{7}\)
c: \(32^{\dfrac{x+5}{x-4}}=0,25\cdot128^{\dfrac{x+17}{x-3}}\)
=>\(2^{\dfrac{5x+25}{x-4}}=2^{-2}\cdot2^{\dfrac{7x+119}{x-3}}\)
=>\(\dfrac{5x+25}{x-4}=-2+\dfrac{7x+119}{x-3}\)
=>\(\dfrac{5x+25}{x-4}=\dfrac{-2x+6+7x+119}{x-3}\)
=>\(\dfrac{5x+25}{x-4}=\dfrac{5x+125}{x-3}\)
=>\(\left(5x+25\right)\left(x-3\right)=\left(5x+125\right)\left(x-4\right)\)
=>\(\left(x+5\right)\left(x-3\right)=\left(x+25\right)\left(x-4\right)\)
=>\(x^2-3x+5x-15=x^2-4x+25x-100\)
=>2x-15=21x-100
=>2x-21x=-100+15
=>-19x=-85
=>\(x=\dfrac{85}{19}\)
Cho \(\log_pq=\sqrt{5}\) . Tính \(\log_{\sqrt{pq}}\left(\dfrac{q}{\sqrt{p}}\right)\)
\(log_{\sqrt{pq}}\left(\dfrac{q}{\sqrt{p}}\right)=2log_{pq}\left(\dfrac{q}{\sqrt{p}}\right)=2log_{pq}q-2log_{pq}\sqrt{p}\)
\(=\dfrac{2}{log_qpq}-log_{pq}p=\dfrac{2}{log_qp+log_qq}-\dfrac{1}{log_ppq}=\dfrac{2}{\dfrac{1}{\sqrt{5}}+1}-\dfrac{1}{log_pp+log_pq}\)
\(=\dfrac{2}{\dfrac{1}{\sqrt{5}}+1}-\dfrac{1}{1+\sqrt{5}}=\dfrac{11-3\sqrt{5}}{4}\)
Giả sử a, b là các số dương thỏa a2 + b2 = 7ab. Chứng minh \(2\log_2\left(\dfrac{a+b}{3}\right)=\log_2a+\log_2b\)
\(a^2+b^2=7ab\Leftrightarrow a^2+b^2+2ab=9ab\)
\(\Leftrightarrow\left(a+b\right)^2=9ab\Leftrightarrow\dfrac{\left(a+b\right)^2}{9}=ab\)
\(\Leftrightarrow\left(\dfrac{a+b}{3}\right)^2=ab\)
Lấy logarit cơ số 2 hai vế:
\(log_2\left(\dfrac{a+b}{3}\right)^2=log\left(ab\right)\)
\(\Leftrightarrow2log_2\left(\dfrac{a+b}{3}\right)=log_2a+log_2b\)
d: \(5^{2x}-7^x-5^{2x}\cdot35+7^x\cdot35=0\)
=>\(\left(5^{2x}-7^x\right)-35\left(5^{2x}-7^x\right)=0\)
=>\(\left(5^{2x}-7^x\right)\cdot\left(-34\right)=0\)
=>\(5^{2x}-7^x=0\)
=>\(5^{2x}=7^x\)
=>\(25^x=7^x\)
=>\(\left(\dfrac{7}{25}\right)^x=1\)
=>x=0
g: \(3\cdot25^{x-2}+\left(3x-10\right)\cdot5^{x-2}+3-x=0\)
=>\(3\cdot\left(5^{x-2}\right)^2-5^{x-2}+\left(3x-9\right)\cdot5^{x-2}-\left(x-3\right)=0\)
=>\(5^{x-2}\left(3\cdot5^{x-2}-1\right)+\left(x-3\right)\left(3\cdot5^{x-2}-1\right)=0\)
=>\(\left(5^{x-2}+x-3\right)\left(3\cdot5^{x-2}-1\right)=0\)
=>\(\left[{}\begin{matrix}5^{x-2}+x-3=0\\3\cdot5^{x-2}-1=0\end{matrix}\right.\)
TH1: \(5^{x-2}+x-3=0\)
Đặt \(A\left(x\right)=5^{x-2}+x-3\)
=>\(A\left(x\right)=\dfrac{1}{25}\cdot5^x+x-3\)
=>\(A'\left(x\right)=\dfrac{1}{25}\cdot5^x\cdot ln5+1>0\)
=>A(x) luôn đồng biến trên R
=>A(x)=0 khi x=2
Th2: \(3\cdot5^{x-2}-1=0\)
=>\(5^{x-2}=\dfrac{1}{3}\)
=>\(x-2=log_5\dfrac{1}{3}\)
=>\(x=2+log_5\left(\dfrac{1}{3}\right)\)
h: \(3\cdot4^x+\left(3x-10\right)\cdot2^x+3-x=0\)
=>\(3\cdot4^x-2^x+\left(3x-9\right)\cdot2^x-\left(x-3\right)=0\)
=>\(2^x\left(3\cdot2^x-1\right)+\left(x-3\right)\left(3\cdot2^x-1\right)=0\)
=>\(\left(3\cdot2^x-1\right)\left(2^x+x-3\right)=0\)
TH1: \(3\cdot2^x-1=0\)
=>\(2^x=\dfrac{1}{3}\)
=>\(x=log\left(\dfrac{1}{3}\right)\)
TH2: \(2^x+x-3=0\)
Đặt \(B\left(x\right)=2^x+x-3\)
=>\(B'\left(x\right)=2^x\cdot ln3+1>0\)
=>B(x) luôn đồng biến trên R
=>B(x)=0 khi x=1
giải phương trình bài này với ạ
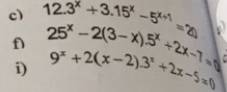
GIẢI PHƯƠNG TRÌNH 3 câu này giúp em ạ
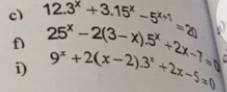
c: \(12\cdot3^x+3\cdot15^x-5^{x+1}=20\)
=>\(12\cdot3^x+3\cdot3^x\cdot5^x-5^x\cdot5-20=0\)
=>\(3^x\cdot3\left(5^x+4\right)-5\left(5^x+4\right)=0\)
=>\(\left(3^{x+1}-5\right)\left(5^x+4\right)=0\)
=>\(3^{x+1}-5=0\)
=>\(3^{x+1}=5\)
=>\(x+1=log_35\)
=>\(x=log_35-1\)
f: \(25^x-2\left(3-x\right)\cdot5^x+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\cdot\left(2x-6\right)+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\left(2x-7\right)+5^x+2x-7=0\)
=>\(5^x\left(5^x+2x-7\right)+\left(5^x+2x-7\right)=0\)
=>\(\left(5^x+1\right)\left(5^x+2x-7\right)=0\)
=>\(5^x+2x-7=0\)
Đặt \(A\left(x\right)=5^x+2x-7\)
=>\(A'\left(x\right)=5^x\cdot ln5+2>0\forall x\)
=>A(x) đồng biến trên R
=>A(x)=0 khi và chỉ khi x=1
i: \(9^x+2\left(x-2\right)\cdot3^x+2x-5=0\)
=>\(\left(3^x\right)^2+3^x\left(2x-5\right)+3^x+2x-5=0\)
=>\(\left(3^x+2x-5\right)\left(3^x+1\right)=0\)
=>\(3^x+2x-5=0\)
Đặt \(B\left(x\right)=3^x+2x-5\)
=>\(B'\left(x\right)=3^x\cdot ln3+2>0\)
=>B(x) luôn đồng biến trên R
=>B(x)=0 khi và chỉ khi x=1
Giải giúp em bài này bằng hình thức tự lụaan với ạ Em cảm ơn nhiều ạ 2^x=x+12
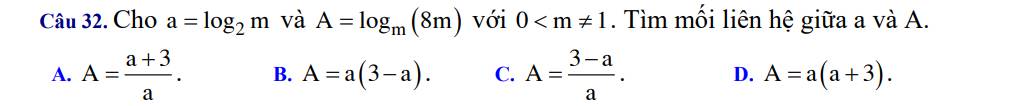 Giải giúp mình câu này với ạ.
Giải giúp mình câu này với ạ.
Câu 32 trong đề thi học kì 1 lớp 12 môn Toán 2022 – 2023 sở GD_ĐT Bình Dương. File đề: https://dethitoan.com.vn/?p=4869
\(A=log_m\left(8m\right)=log_mm+log_m8\)
\(=1+log_m8\)
\(=1+\dfrac{1}{log_8m}=1+\dfrac{1}{log_{2^3}m}=1+\dfrac{1}{\dfrac{1}{3}\cdot log_2m}\)
\(=1+\dfrac{1}{\dfrac{1}{3}a}=1+1:\dfrac{a}{3}=1+\dfrac{3}{a}=\dfrac{a+3}{a}\)
=>Chọn A
Tổng các nghiệm thực của phương trình 7^(8x-x^2)=3^(2x+5) bằng a - logb(c) với a, b,c là các số nguyên dương bé nhất . Giá trị của a+b-c
Giải giúp mình vs ạ.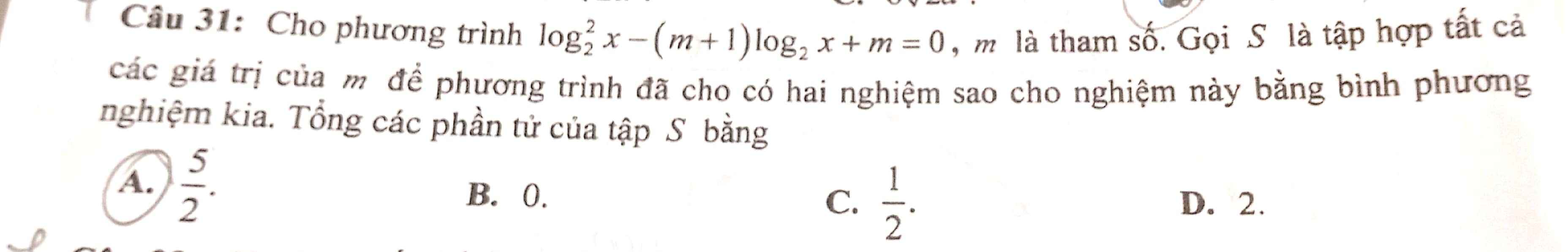
ĐKXĐ: \(x>0\)
\(log_2^2x-m.log_2x-log_2x+m=0\)
\(\Leftrightarrow log_2x\left(log_2x-m\right)-\left(log_2x-m\right)=0\)
\(\Leftrightarrow\left(log_2x-1\right)\left(log_2x-m\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=2^m\end{matrix}\right.\)
TH1: \(x_1=x_2^2\Leftrightarrow2=\left(2^m\right)^2=2^{2m}\Rightarrow2m=1\Rightarrow m=\dfrac{1}{2}\)
TH2: \(x_2=x_1^2\Rightarrow2^m=2^2\Rightarrow m=2\)
\(\Rightarrow2+\dfrac{1}{2}=\dfrac{5}{2}\)