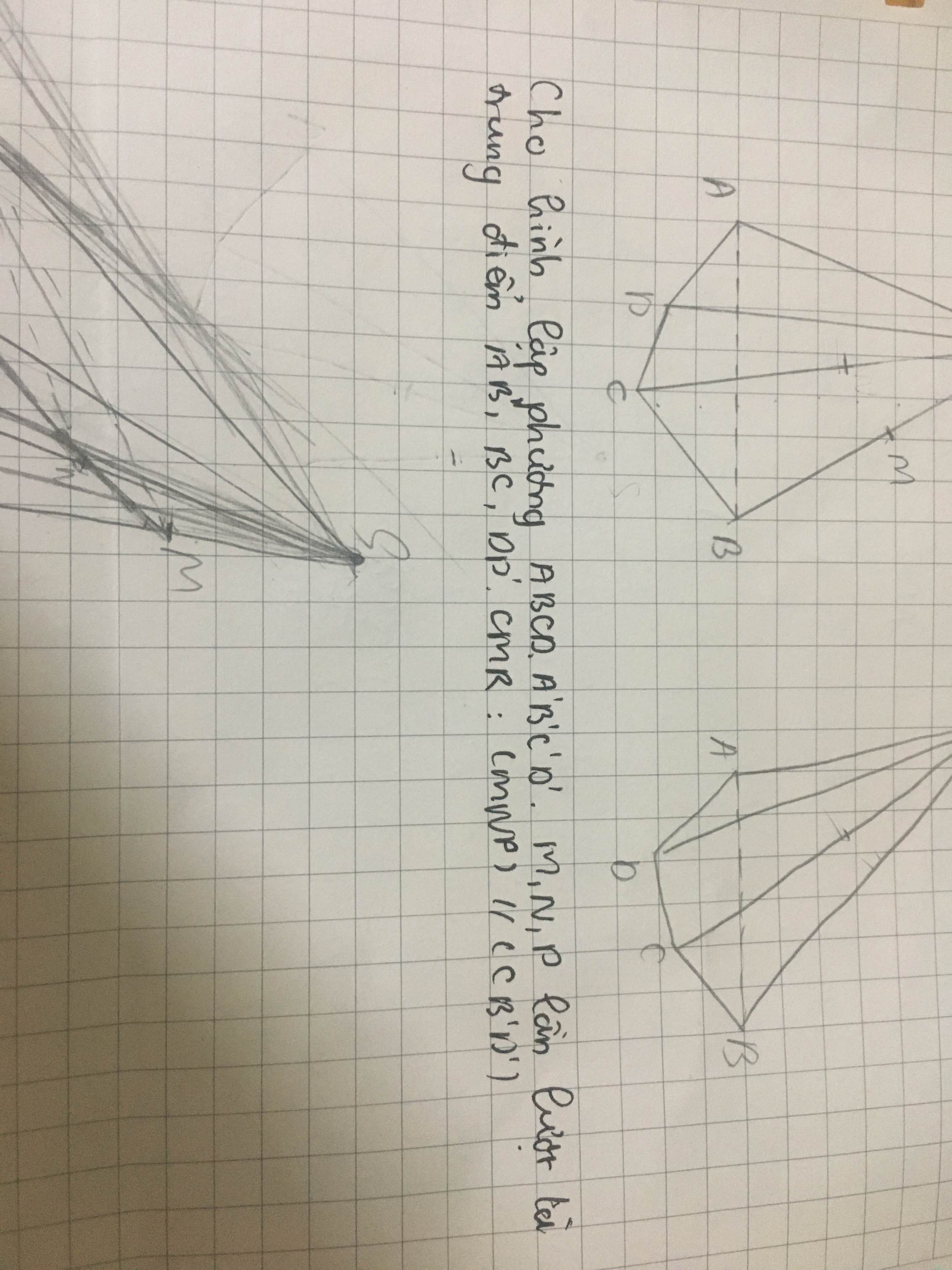
1) dfrac{AM}{AB}dfrac{AN}{AC} →MN//AC . Day la dinh ly Ta - let hay Ta - let dao
Đọc tiếp
1) \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\) →MN//AC . Day la dinh ly Ta - let hay Ta - let dao
Bài 4: Hai mặt phẳng song song
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: (x+1)^2+(y-2)^2=4. Ảnh của đường tròn (C) quá phép vị tự tâm O tỉ số -3 có bán kính là: A.4 B.12 C.-12 D.6
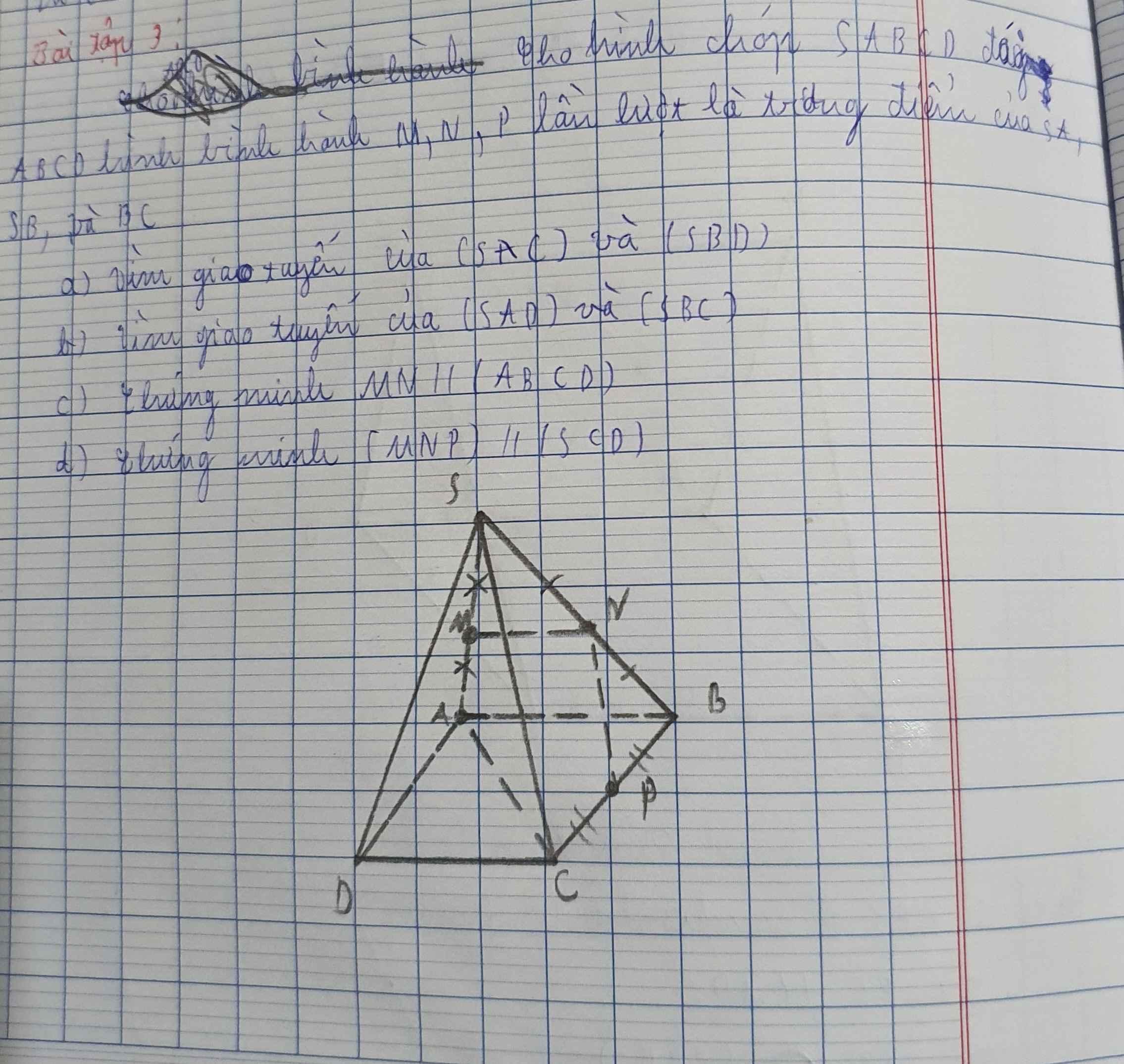
2. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M và N là
trung điểm của AB và SC
a)Tìm các giao tuyến (SAC) và (SBD).
b)Tìm các giao tuyến (SAB) và (SCD).
c)Chứng minh rằng MN //(SAD)
d)Chứng minh rằng đường thẳng AN đi qua trọng tâm của tam giác SBD
e) Gọi P là trung điểm của SA. Dựng thiết diện của hình chóp với mặt
phẳng (MNP)
a: Gọi O là giao của AC và BD
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
b: Kẻ Sx//AD//BC
=>(SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
c: Xét ΔSAB co SM/SA=SN/SB
nên MN//AB
=>MN//(ABCD)
Đúng 0
Bình luận (0)
19 tháng 2 2023 lúc 20:51
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành . Gọi M, N, P lần lượt là trung điểm các đoạn thẳng SA, BC, CD gọi K là điểm bất kì nằm trên OM chứng minh KN//(SCD)
25 tháng 8 2023 lúc 14:45
giúp mình bài này với ạ.
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm cảu AB, SC; E là trung điểm SA. Thiết diện hình chóp khi cắt bởi mặt phẳng ( EMN ).
Gọi P là giao điểm của mặt phẳng (EMN) với cạnh AB. Ta có ME là đường trung bình của tam giác SAB, nên ta có ME song song với đoạn thẳng AB và ME = 1/2 * AB. Tương tự, ta cũng có MN song song với cạnh SC và MN = 1/2 * SC. Vì EMN là tam giác đều, nên ta có EP = EN = NP = 1/3 * EMN.
Vì E là trung điểm của SA, nên ta có SE = 1/2 * SA. Vì SN là đường trung bình của tam giác SCA, nên ta có SN = 1/2 * SC.
Từ các thông tin trên, ta có thể xác định các điểm P, E, và N trên hình chóp S.ABCD. Sau đó, ta vẽ đường thẳng EN và vẽ đường thẳng qua P song song với đáy ABCD, giao điểm của hai đường thẳng này là điểm M.
Vậy, thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (EMN) là một hình bình hành có các đỉnh là các điểm E, M, N và các cạnh là các đoạn thẳng EM, MN, NE.
Đúng 0
Bình luận (0)
cho hình chóp sabcd có đáy là hình bình hành, gọi G là trọng tâm tam giác SAD, gọi M thuộc cạnh cd hỏa mãn 3MD=CD. cmr MG//( SBC)
Cho h.chóp S.ABCD có đáy ABCD là hình thang (đáy lớn AD). M là trọng tâm △SAD.
N ϵ AC: AN = 1/3 AC.
P ϵ CD: DP = 1/3 DC.
Chứng minh: (MNP) // (SBC).