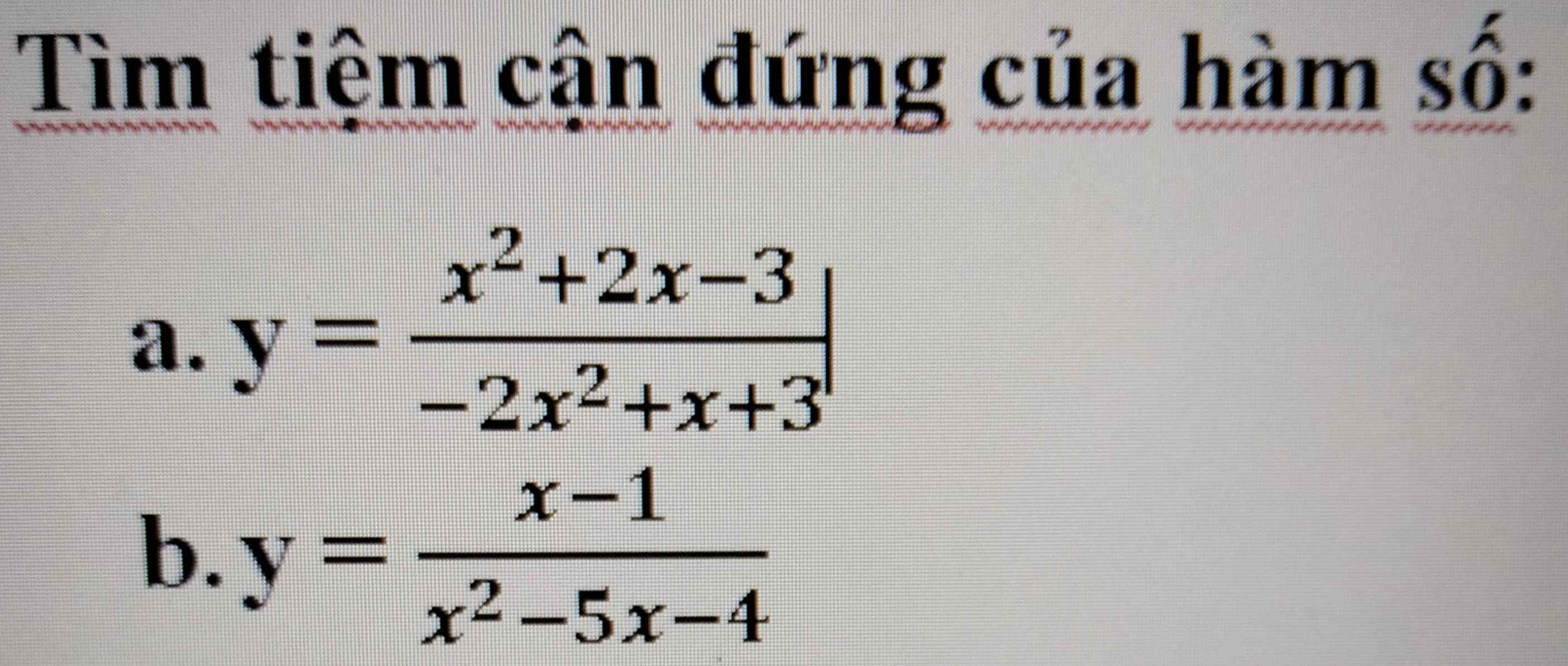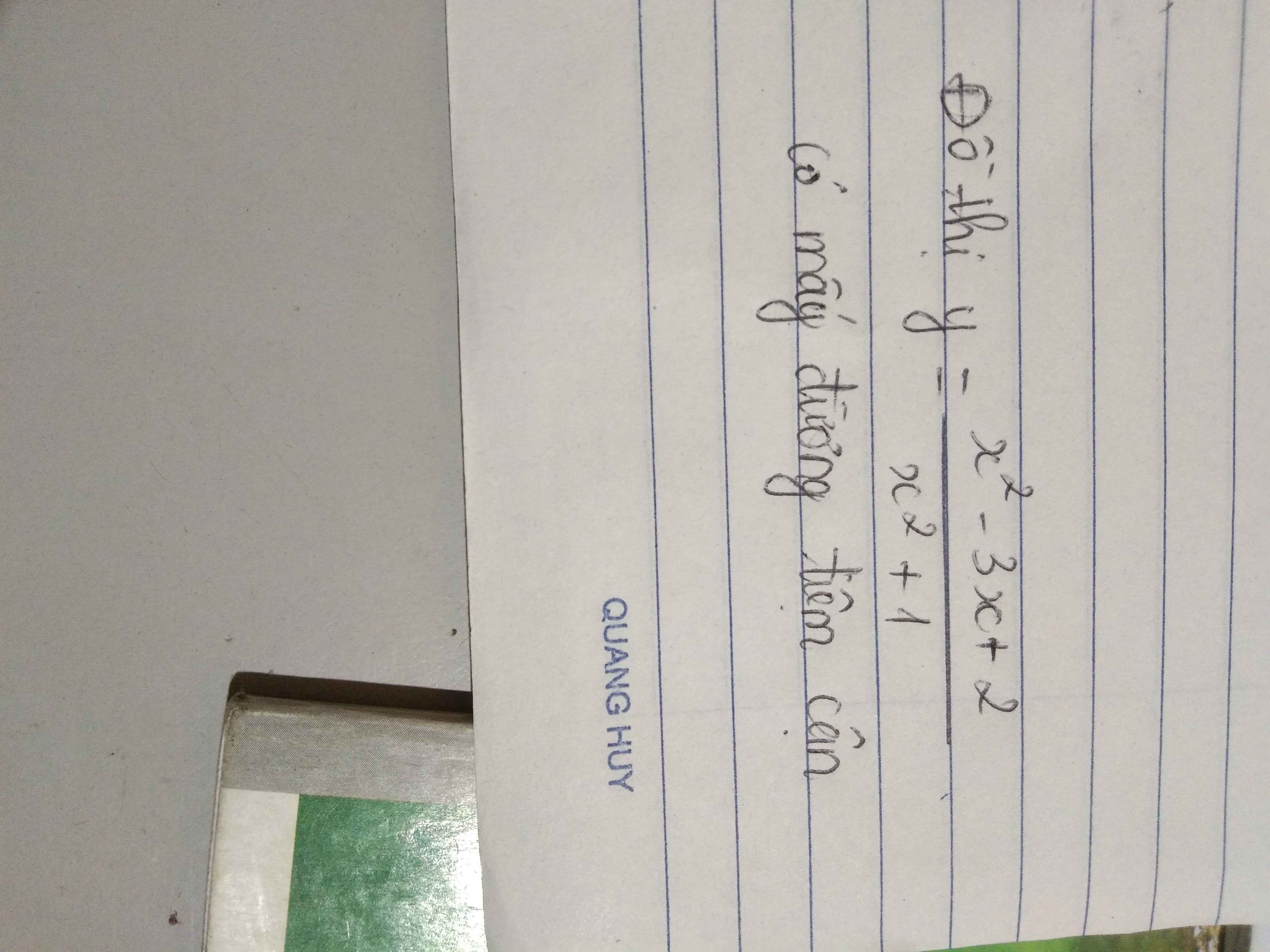tìm tiệm cận đứng và tiệm cận ngang
a, lim y= 1/2
x→ -∞
b, lim y= -∞
x=→3
Bài 4: Đường tiệm cận
a) \(\lim\limits_{x\rightarrow-\infty}y=\dfrac{1}{2}\)
Tiệm cận ngang là \(y=\dfrac{1}{2}\)
b) \(\lim\limits_{x\rightarrow3}y=-\infty\)
Tiệm cận đứng \(x=3\)
Đúng 1
Bình luận (0)
1, Tìm tất cả giá trị thực m sao cho đths \(y=\dfrac{x+1}{\sqrt{mx^2+1}}\)có hai tiệm cận ngang
A. ko có gtrị thực nào của m thỏa mãn yêu cầu đề bài
B.m<0 C. m=0 D.m>0
2, Tìm tất cả giá trị thực m sao cho đths \(y=\dfrac{x-3}{x+\sqrt{mx^2+4}}\)có đúng một tiệm cận ngang
A.m=0,m=1 B.m≥0 C.m=1 D.m=0
Đọc tiếp
Lời giải:
\(\lim\limits_{x\to \pm \infty}y=\lim\limits_{x\to \pm \infty}\frac{mx+1}{2m+1-x}=-m\) nên $y=-m$ là TCN của đths
\(\lim\limits_{x\to 2m+1}y=\lim\limits_{x\to 2m+1}\frac{mx+1}{2m+1-x}=\infty\) nên $x=2m+1$ là TCĐ của đths
2 TC tạo với trục $Ox, Oy$ một HCN có độ dài $|m|, |2m+1|$
Ta có:
$|m(2m+1)|=3$
$\Leftrightarrow 2m^2+m=3$ hoặc $2m^2+m=-3$
$\Leftrightarrow m=1$ hoặc $m=\frac{-3}{2}$
Đúng 0
Bình luận (0)
Cho \(\left\{{}\begin{matrix}u_n=1\\u_{n+1}=\sqrt{1+2u_nu_{n+1}}\end{matrix}\right.\)
CMR u2019 là số vô tỷ
Giả sử tồn tại 1 số \(k>1\) sao cho \(u_k\) là số hữu tỉ
\(\Rightarrow u_k=\sqrt{1+2u_k.u_{k-1}}\Rightarrow u_k^2=1+2u_k.u_{k-1}\)
\(\Rightarrow\dfrac{u_k}{2}-\dfrac{1}{2u_k}=u_{k-1}\)
Do \(u_k\) hữu tỉ \(\Rightarrow\dfrac{u_k}{2}-\dfrac{1}{2u_k}\) hữu tỉ
\(\Rightarrow u_{k-1}\) hữu tỉ
Theo nguyên lý quy nạp, ta suy ra mọi số hạng trong dãy đều là số hữu tỉ
Nhưng \(u_2=1+\sqrt{2}\) là số vô tỉ (trái với giả thiết)
Vậy điều giả sử là sai hay với mọi \(k>1\) thì \(u_k\) luôn là số vô tỉ
Hay \(u_{2019}\) là số vô tỉ
Đúng 1
Bình luận (7)
Chắc đề phải là \(u_1=1\) mới đúng (nãy ko để ý, ai cho \(u_n=1\) bao giờ, điều đó đồng nghĩa mọi số hạng của dãy đều bằng 1, phi lý)
Thử truy hồi theo lượng giác để tìm CTTQ của dãy (mặc dù điều này sẽ không chứng minh được \(u_k\) hữu tỉ, vì chứng minh 1 giá trị lương giác là hữu tỉ rất khó)
Hiển nhiên dãy đã cho là dãy dương
\(u_{n+1}^2=1+2u_nu_{n+1}>1+u_nu_{n+1}\Rightarrow u_{n+1}>\dfrac{1}{u_{n+1}}+u_n\)
\(\Rightarrow u_{n+1}-u_n>\dfrac{1}{u_{n+1}}>0\)
Do đó: \(u_{n+1}^2=1+2u_nu_{n+1}\Leftrightarrow u_{n+1}^2-2u_nu_{n+1}+u_n^2=u_n^2+1\)
\(\Leftrightarrow\left(u_{n+1}-u_n\right)^2=u_n^2+1\Rightarrow u_{n+1}=u_n+\sqrt{u_n^2+1}\)
Có: \(u_1=1=tan\dfrac{\pi}{4}\)
\(u_2=tan\dfrac{\pi}{4}+\sqrt{tan^2\dfrac{\pi}{4}+1}=tan\dfrac{\pi}{4}+\dfrac{1}{cos\dfrac{\pi}{4}}=\dfrac{sin\dfrac{\pi}{4}+1}{cos\dfrac{\pi}{4}}=\dfrac{sin\dfrac{\pi}{8}+cos\dfrac{\pi}{8}}{cos\dfrac{\pi}{8}-sin\dfrac{\pi}{8}}\)
\(=tan\left(\dfrac{\pi}{8}+\dfrac{\pi}{4}\right)=tan\left(\dfrac{\pi}{2}\left(\dfrac{1}{2}+\dfrac{1}{2^2}\right)\right)\)
\(u_3=tan\left(\dfrac{\dfrac{\pi}{8}+\dfrac{\pi}{4}}{2}+\dfrac{\pi}{4}\right)=tan\left(\dfrac{\pi}{2}\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}\right)\right)\)
\(u_4=tan\left(\dfrac{\dfrac{\pi}{16}+\dfrac{\pi}{4}\left(1+\dfrac{1}{2}\right)}{2}+\dfrac{\pi}{4}\right)=tan\left(\dfrac{\pi}{2}\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}\right)\right)\)
Vậy có thể tổng quát được:
\(u_n=tan\left(\dfrac{\pi}{2}\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^n}\right)\right)=tan\left(\dfrac{\pi}{2}\left(1-\dfrac{1}{2^n}\right)\right)=tan\left(\dfrac{\pi}{2}-\dfrac{\pi}{2^{n+1}}\right)\)
\(\Rightarrow u_{10}=tan\left(\dfrac{\pi}{2}-\dfrac{\pi}{2^{11}}\right)\)
Đúng 0
Bình luận (0)
a.
\(-2x^2+x+3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\) (và đều không phải nghiệm của tử số)
\(\Rightarrow x=-1\) và \(x=\dfrac{3}{2}\) là 2 TCĐ
b.
\(x^2-5x-4=0\Rightarrow x=\dfrac{5\pm\sqrt{41}}{2}\)
\(\Rightarrow x=\dfrac{5\pm\sqrt{41}}{2}\) là 2 TCĐ
Đúng 0
Bình luận (0)
y=2x-3 / x+2
Hàm số \(y=2x-\dfrac{3}{x}+2\) có tiệm cận đứng là đường thẳng x=0, không có tiệm cận ngang.
Hàm số \(y=2x-\dfrac{3}{x+2}\) có tiệm cận đứng là đường thẳng x= -2, không có tiệm cận ngang.
Hàm số \(y=\dfrac{2x-3}{x+2}\) có tiệm cận ngang là đường thẳng y=2, tiệm cận đứng là đường thẳng x= -2.
Đúng 0
Bình luận (0)
Tìm m thuộc R để đồ thị hàm số y= (3-x)/ (2x+2m) có tiệm cận đứng là đường thẳng đi qua A(2:0)
A. m=1.
B. m= - 2.
C.m=− 1.
D. m=0.
Lời giải:
Theo đề thì cần tìm $m$ để đths đã cho cho TCĐ $x=2$
Điều này xảy ra khi mà $2x+2m=0$ tại $x=2$
$\Leftrightarrow m=-x=-2$
Đáp án B.
Đúng 0
Bình luận (0)