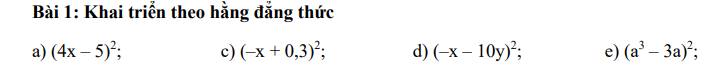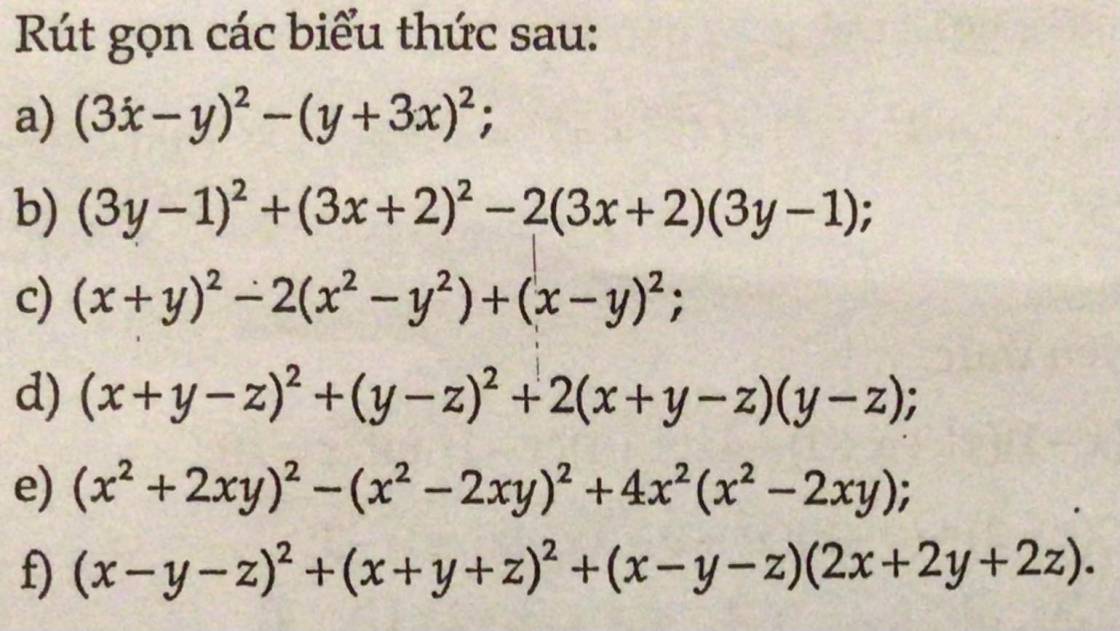Bài 3: Những hằng đẳng thức đáng nhớ

a: \(50.5^2-50.4^2=\left(50.5-50.4\right)\cdot\left(50.5+50.4\right)\)

\(=100.9\cdot0.1=10.09\)

b; \(202\cdot198=\left(200+2\right)\left(200-2\right)\)

\(=200^2-2^2=40000-4=39996\)

c: \(10.2^2=\left(10+0.2\right)^2\)

\(=10^2+2\cdot10\cdot0.2+0.2^2\)

\(=100+0.04+4=104.04\)

d: \(101^2-202\cdot71+71^2\)

\(=101^2-2\cdot101\cdot71+71^2\)

\(=\left(101-71\right)^2=50^2=2500\)

Ta có:

\(x^3+x^2z-xyz+y^2z+y^3\)

\(=\left(x^3+y^3\right)+\left(x^2z-xyz+y^2z\right)\)

\(=\left(x+y\right)\left(x^2-xy+y^2\right)+z\left(x^2-xy+y^2\right)\)

\(=\left(x+y+z\right)\left(x^2-xy+y^2\right)\)

\(=0\cdot\left(x^2-xy+y^2\right)\)

\(=0\left(dpcm\right)\)

a: \(A=2x^2-5x-2x\left(x+1\right)\)

\(=2x^2-5x-2x^2-2x\)

=-7x

b: \(B=\left(x+2y\right)\left(x-2y\right)-4y\left(x-y\right)\)

\(=x^2-4y^2-4xy+4y^2\)

\(=x^2-4xy\)

c: \(C=\left(2x-8\right)\left(x^2+4x+16\right)-2x\left(x^2-2\right)\)

\(=2\left(x-4\right)\left(x^2+4x+16\right)-2x\left(x^2-2\right)\)

\(=2\left(x^3-64\right)-2x^3+4x\)

\(=2x^3-128-2x^3+4x=4x-128\)

\(D=2023-8x+2y+4xy-y^2-5x^2\)

\(=-\left(y^2+5x^2-4xy-2y+8x-2023\right)\)

\(=-\left(y^2-2.y.\left(2x+1\right)+\left(2x+1\right)^2-\left(2x+1\right)^2+5x^2+8x-2023\right)\)

\(=-\left[\left(y-2x-1\right)^2-4x^2-4x-1+5x^2+8x-2023\right]\)

\(=-\left[\left(y-2x-1\right)^2+x^2+4x-2024\right]\)

\(=-\left[\left(y-2x-1\right)^2+\left(x+2\right)^2\right]+2028\)

Vì \(-\left[\left(y-2x-1\right)^2+\left(x+2\right)^2\right]\le0\forall x,y\)

\(MaxD=2028\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)

a) \(\left(4x-5\right)^2\)

\(=\left(4x\right)^2-2\cdot4x\cdot5+5^2\)

\(=16x^2-40x+25\)

b) \(\left(-x+0,3\right)^2\)

\(=\left(-x\right)^2+2\cdot\left(-x\right)\cdot0,3+\left(0,3\right)^2\)

\(=x^2-0,6x+0,09\)

c) \(\left(-x-10y\right)^2\)

\(=\left(-x\right)^2+2\cdot\left(-x\right)\cdot\left(-10y\right)+\left(-10y\right)^2\)

\(=x+20xy+100y^2\)

d) \(\left(a^3-3a\right)^2\)

\(=\left(a^3\right)^2-2\cdot a^3\cdot3a+\left(3a\right)^2\)

\(=a^6-6a^4+9a^2\)

a: \(\left(4x-5\right)^2=\left(4x\right)^2-2\cdot4x\cdot5+5^2=16x^2-40x+25\)

c: \(\left(-x+0.3\right)^2=\left(-x\right)^2+2\cdot\left(-x\right)\cdot0.3+0.3^2\)

\(=x^2-0.6x+0.09\)

d: \(\left(-x-10y\right)^2=\left(x+10y\right)^2\)

\(=x^2+2\cdot x\cdot10y+\left(10y\right)^2\)

\(=x^2+20xy+100y^2\)

e: \(\left(a^3-3a\right)^2\)

\(=\left(a^3\right)^2-2\cdot a^3\cdot3a+\left(3a\right)^2\)

\(=a^6-6a^4+9a^2\)

\(F=x^2+6x-5=x^2+6x+9-14=\left(x+3\right)^2-14\)

\(G=x^2-8x-5=x^2-8x+16-21=\left(x-4\right)^2-21\)

\(H=x^2-10x+31=x^2-10x+25+6=\left(x-5\right)^2+6\)

\(K=x^2-12x+9=x^2-12x+36-27\)

\(=\left(x-6\right)^2-27\)

\(M=x^2-14x+20=x^2-14x+49-29\)

\(=\left(x-7\right)^2-29\)

\(N=x^2-16x+25=x^2-16x+64-39\)

\(=\left(x-8\right)^2-39\)

\(P=9x^2+12x+5\)

\(=9x^2+12x+4+1=\left(3x+2\right)^2+1\)

\(S=9x^2+6x+3=9x^2+6x+1+2=\left(3x+1\right)^2+2\)

(x + y)² = x² + 2xy + y²

a) \((a+y)^3=a^3+3a^2y+3ay^2+y^3\)

b) \((x-b)^3=x^3-3x^2b+3xb^2-b^3\)

`(x+y)^2 -2(x+y)(x-y)+(x-y)^2`

\(=\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =\left(2y\right)^2\\ =4y^2\)

a) \(\left(3x-y\right)^2-\left(y+3x\right)^2=\left(3x-y+y+3x\right)\left(3x-y-y-3x\right)\)

\(=6x.\left(-2y\right)=-12xy\)

b) \(\left(3y-1\right)^2+\left(3x+2\right)^2-2\left(3x+2\right)\left(3y-1\right)\)

\(=\left(3y-1-3x-2\right)^2=\left(3y-3x-3\right)^2=9\left(x-y-1\right)^2\)

c) \(\left(x+y\right)^2-2\left(x^2-y^2\right)+\left(x-y\right)^2\)

\(=\left(x+y-x+y\right)^2=4y^2\)

d) \(\left(x+y-z\right)^2+\left(y-z\right)^2+2\left(x+y-z\right)\left(y-z\right)\)

\(=\left(x+y-z+y-z\right)^2=\left(x+2y-2z\right)^2\)

e) \(\left(x^2+2xy\right)^2-\left(x^2-2xy\right)^2+4x^2\left(x^2-2xy\right)\)

\(=\left(x^2+2xy-x^2+2xy\right)\left(x^2+2xy+x^2-2xy\right)+4x^2\left(x^2-2xy\right)\)

\(=8x^3y+4x^2\left(x^2-2xy\right)=4x^2\left(2xy+x^2-2xy\right)=4x^4\)

f) \(\left(x-y-z\right)^2+\left(x+y+z\right)^2+\left(x-y-z\right)\left(2x+2y+2z\right)\)

\(=\left(x-y-z+x+y+z\right)^2=4x^2\)

Lời giải:

a.

$=(3x-y-y-3x)(3x-y+y+3x)=-2y.6x=-12xy$

b.

$=[(3y-1)-(3x+2)]^2=(3y-3x-3)^2=9(y-x-1)^2$

c.

$=(x+y)^2-2(x-y)(x+y)+(x-y)^2=[(x+y)-(x-y)]^2=(2y)^2=4y^2$
d.

$=[(x+y-z)+(y-z)]^2=(x+2y-2z)^2$

e.

$=(x^2+2xy-x^2+2xy)(x^2+2xy+x^2-2xy)+4x^2(x^2-2xy)$

$=4xy.2x^2+4x^2(x^2-2xy)=8x^3y+4x^2(x^2-2xy)$

$=4x^2(2xy+x^2-2xy)=4x^2.x^2=4x^4$

f.

$=(x-y-z)^2+(x+y+z)^2+2(x-y-z)(x+y+z)$

$=[(x-y-z)+(x+y+z)]^2=(2x)^2=4x^2$