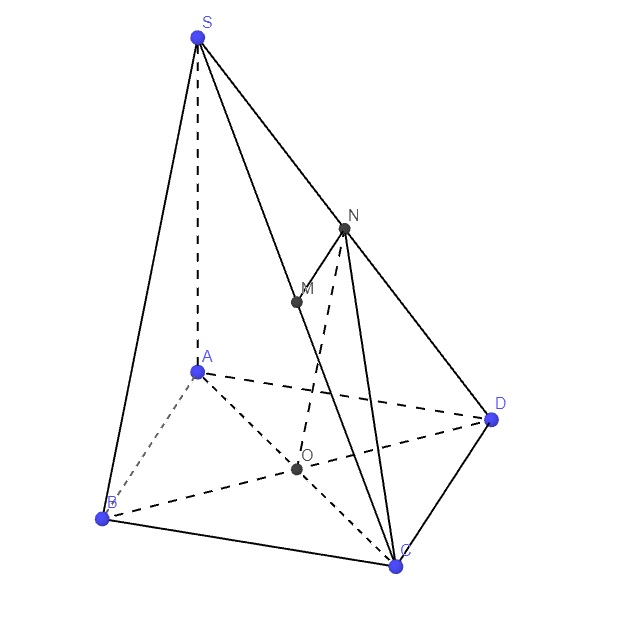
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy . Chứng minh rằng BD vuông góc SAC Gọi M N là trung điểm của SC SD chứng minh MN vuông góc với SAD Cho SA= a√3 tính góc giữa hai đường thẳng SB và CN
Bài 3: Đường thẳng vuông góc với mặt phẳng
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\\BD\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp BD\)
Lại có \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\) (1)
M là trung điểm SC, N là trung điểm SD \(\Rightarrow\) MN là đường trung bình tam giác SCD
\(\Rightarrow MN||CD\) (2)
(1);(2) \(\Rightarrow MN\perp\left(SAD\right)\)
Gọi O là tâm đáy \(\Rightarrow ON\) là đường trung bình tam giác SBD
\(\Rightarrow ON||SB\Rightarrow\widehat{\left(SB,CN\right)}=\widehat{\left(ON,CN\right)}=\widehat{ONC}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
\(ON=\dfrac{1}{2}SB\Rightarrow ON=a\)
\(OC=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
\(SD=\sqrt{SA^2+AD^2}=2a\Rightarrow ND=\dfrac{1}{2}SD=a\)
\(\Rightarrow CN=\sqrt{CD^2+ND^2}=a\sqrt{2}\)
\(cos\widehat{ONC}=\dfrac{ON^2+CN^2-OC^2}{2ON.CN}=\dfrac{5\sqrt{2}}{8}\)
\(\Rightarrow\widehat{ONC}\approx27^053'\)
Đúng 3
Bình luận (0)
giải giúp em ạ
3.
a.
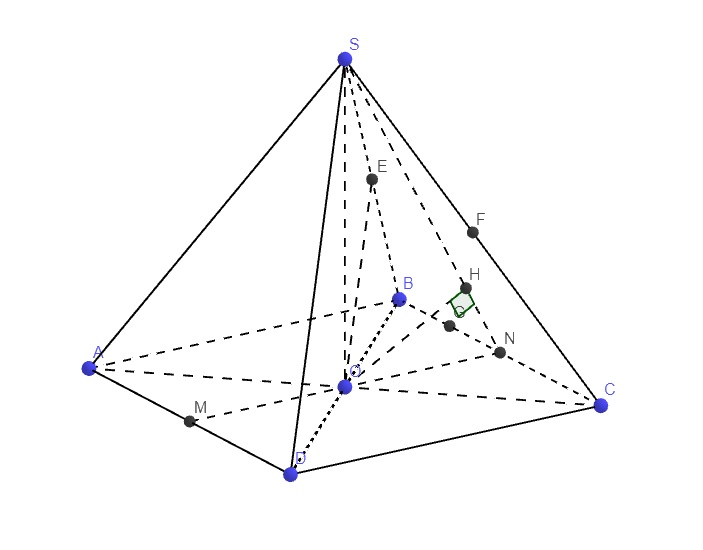
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\\BD\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SO\perp BD\)
\(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\)
b.
M là trung điểm AD, N là trung điểm BC \(\Rightarrow MN||AB\Rightarrow MN\perp BC\)
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
Mà \(SO\in\left(SMN\right)\Rightarrow BC\perp\left(SMN\right)\)
\(\Rightarrow BC\perp SM\)
Lại có \(OH\in\left(SMN\right)\Rightarrow BC\perp OH\)
Theo giả thiết \(OH\perp SN\)
\(\Rightarrow OH\perp\left(SBC\right)\Rightarrow OH\perp SB\)
c.
\(\left\{{}\begin{matrix}AC\perp BD\\SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\)
Hay \(OC\perp\left(SBD\right)\)
\(\Rightarrow\) Góc giữa (SBC) và (SBD) là góc giữa 2 đường thẳng OC và OH
Hay \(\left(\left(SBD\right),\left(SBD\right)\right)=\widehat{COH}\)
\(OB=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow SO=\sqrt{SB^2-OB^2}=\dfrac{a\sqrt{6}}{2}\)
\(ON=\dfrac{1}{2}AB=\dfrac{a}{2}\Rightarrow OH=\dfrac{SO.ON}{\sqrt{SO^2+ON^2}}=\dfrac{a\sqrt{42}}{14}\)
\(OH\perp\left(SBC\right)\Rightarrow OH\perp CH\Rightarrow\Delta OCH\) vuông tại H
\(\Rightarrow cos\widehat{COH}=\dfrac{OH}{OC}=\dfrac{OH}{OB}=\dfrac{\sqrt{21}}{7}\)
\(\Rightarrow\widehat{COH}\approx49^06'\)
Đúng 3
Bình luận (0)
3d.
Gọi E là trung điểm SB \(\Rightarrow\) OE là đường trung bình tam giác SBD
\(\Rightarrow OE||SD\)
\(\Rightarrow\left(OH,SD\right)=\left(OH,OE\right)=\widehat{EOH}\)
\(OE=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\) (trung tuyến ứng với cạnh huyền)
\(OH\perp\left(SBC\right)\Rightarrow OH\perp EH\Rightarrow\Delta OEH\) vuông tại H
\(cos\widehat{EOH}=\dfrac{OH}{OE}=\dfrac{\sqrt{21}}{7}\Rightarrow\widehat{EOH}\approx49^06'\)
e.
Gọi F là trung điểm SC, G là trung điểm BN
\(\Rightarrow OF\) là đường trung bình tam giác SAC và OG là đường trung bình tam giác BDN
\(\Rightarrow\left\{{}\begin{matrix}OF||SA\\OG||DN\end{matrix}\right.\) \(\Rightarrow\left(SA,DN\right)=\left(OF,OG\right)=\widehat{FOG}\)
\(OF=\dfrac{1}{2}SA=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\)
\(OG=\dfrac{1}{2}DN=\dfrac{1}{2}\sqrt{DC^2+CN^2}=\dfrac{a\sqrt{5}}{4}\)
\(cos\widehat{SCN}=\dfrac{CN}{SC}=\dfrac{\sqrt{2}}{4}\)
\(CF=\dfrac{1}{2}SC=\dfrac{a\sqrt{2}}{2}\) ; \(CG=CN+NG=\dfrac{3}{4}BC=\dfrac{3a}{4}\)
\(\Rightarrow GF=\sqrt{CF^2+CG^2-2CF.CG.cos\widehat{SCN}}=\dfrac{a\sqrt{11}}{4}\)
\(\Rightarrow cos\widehat{FOG}=\dfrac{OF^2+OG^2-FG^2}{2OF.OG}=\dfrac{\sqrt{10}}{20}\)
\(\Rightarrow\widehat{FOG}\approx80^054'\)
Đúng 3
Bình luận (1)
Xem thêm câu trả lời
 giải giúp em ạ
giải giúp em ạ
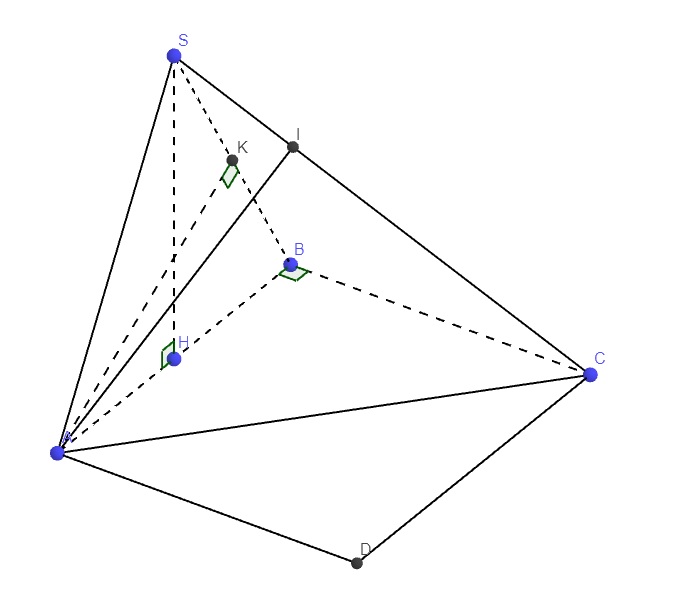
a.
\(\left\{{}\begin{matrix}SH\perp\left(ABC\right)\\BC\in\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow SH\perp BC\)
Lại có \(AB\perp BC\left(gt\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
\(AK\in\left(SAB\right)\Rightarrow BC\perp AK\)
Tam giác ABC đều mà K là trung điểm SB
\(\Rightarrow AK\perp SB\)
\(\Rightarrow AK\perp\left(SBC\right)\)
b.
\(\left\{{}\begin{matrix}AK\in\left(AKI\right)\\AK\perp\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\left(AKI\right)\perp\left(SBC\right)\)
c.
\(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\\BC=\left(SBC\right)\cap\left(ABC\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
Mà tam giác SAB đều \(\Rightarrow\widehat{SBA}=60^0\)
d.
Dựng hình chữ nhật ABCD \(\Rightarrow AB||CD\Rightarrow\left(SC,AB\right)=\left(SC,CD\right)=\widehat{SCD}\)
\(SC=\sqrt{SB^2+BC^2}=2a\)
\(SD=\sqrt{SA^2+AD^2}=\sqrt{SB^2+BC^2}=2a\)
\(CD=AB=a\)
\(\Rightarrow cos\widehat{SCD}=\dfrac{SC^2+CD^2-SD^2}{2SC.CD}=\dfrac{1}{4}\)
\(\Rightarrow\widehat{SCD}\approx75^031'\)
e.
\(AC=\sqrt{AB^2+BC^2}=2a\)
\(cos\widehat{BAC}=\dfrac{AB}{AC}=\dfrac{1}{2}\)
\(\overrightarrow{SB}.\overrightarrow{AC}=\left(\overrightarrow{SH}+\overrightarrow{HB}\right).\overrightarrow{AC}=\overrightarrow{SH}.\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{1}{2}AB.AC.cos\widehat{BAC}=\dfrac{1}{2}.a.2a.\dfrac{1}{2}=\dfrac{a^2}{2}\)
\(\Rightarrow cos\left(AC,SB\right)=\dfrac{\left|\overrightarrow{SB}.\overrightarrow{AC}\right|}{SB.AC}=\dfrac{1}{4}\)
Đúng 3
Bình luận (0)
Mọi người giúp mình bài này với ạ, mình cảm ơn!Bài tập: Cho hình lập phương ABCD.ABCD. Chứng minh mặt phẳng left(ABDright) song song với mặt phẳng left(CBDright). Tìm điểm M trên đoạn BD và điểm N trên đoạn CD sao cho đường thẳng MN vuông góc với mặt phẳng left(ABDright).
Đọc tiếp
Mọi người giúp mình bài này với ạ, mình cảm ơn!
Bài tập: Cho hình lập phương \(ABCD.A'B'C'D'\). Chứng minh mặt phẳng \(\left(A'BD\right)\) song song với mặt phẳng \(\left(CB'D'\right)\). Tìm điểm \(M\) trên đoạn \(BD\) và điểm \(N\) trên đoạn \(CD'\) sao cho đường thẳng \(MN\) vuông góc với mặt phẳng \(\left(A'BD\right)\).
Cho hình tứ diện ABCD có AB ⊥ (BCD), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD. Chứng minh rằng: HK ⊥ (ACD).
Gọi BM là đường cao của BCD \(\Rightarrow BC\perp\left(ABM\right)\Rightarrow CD\perp AM\)
\(\Rightarrow H\) thuộc BM và K thuộc AM nên \(CD\perp HK\)
Tương tự kẻ đường cao từ D qua H (suy ra \(DH\perp\left(ABC\right)\Rightarrow DH\perp AC\)) và qua K (suy ra \(DK\perp AC\)) \(\Rightarrow AC\perp\left(DHK\right)\Rightarrow AC\perp HK\)
Đúng 2
Bình luận (0)
Cho tứ diện OABC có OA, OB , OC đôi một vuông góc với nhau a, CM: OA vuông góc với (OBC) b, gọi OK,OH lần lượt là đường cao của ∆OBC và ∆OAK. CM : OH vuông góc với (ABC) c, H là trực tâm của ∆ABC
a: OA\(\perp\)OB
OA\(\perp\)OC
OB,OC cùng thuộc mp(OBC)
Do đó: OA\(\perp\)(OBC)
b: Ta có: BC\(\perp\)AK
BC\(\perp\)AO
AK,AO cùng thuộc mp(AKO)
Do đó: BC\(\perp\)(AKO)
=>BC\(\perp\)OH
Ta có: OH\(\perp\)BC
OH\(\perp\)AK
AK,BC cùng thuộc mp(ABC)
Do đó: OH\(\perp\)(ABC)
Đúng 0
Bình luận (0)
Cho hình chóp SABCD, đáy ABCD là hình vuông, SA vuông ABCD.
a) chứng minh rằng: CD vuông (SAD)
b) chứng minh: BC vuông (SAB)
c) chứng minh: AB vuông (SAD)
d) chứng minh: AD vuông (SAB)
e) chứng minh: BD vuông (SAC)
a: Ta có: CD\(\perp\)AD(ABCD là hình vuông)
CD\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
b: Ta có: BC\(\perp\)AB(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
AB,SA cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
c: AB\(\perp\)AD(ABCD là hình vuông)
AB\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: AB\(\perp\)(SAD)
d: AD\(\perp\)AB
AD\(\perp\)SA(SA\(\perp\)(ABCD)))
SA,AB cùng thuộc mp(SAB)
Do đó: AD\(\perp\)(SAB)
e: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
Đúng 1
Bình luận (0)
Cho h/c ABCD có ΔABC đều. M là trung điểm CD, AG⊥(BCD) tại G, biết G ϵ BM.
cm: AB⊥CD
Cho h/c ABCD có ΔABC đều. M là trung điểm CD, AG⊥(BCD) tại G, biết G ϵ BM.
cm: AB⊥CD
Cho h/c SABCD có đáy ABCD là hình thang vuông tại A, B, SA⊥(ABCD), AD=2a, AB=BC=a
cm: a) CD⊥(SAC)
b) CD⊥ SC
a: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(AC^2=a^2+a^2=2a^2\)
=>\(AC=a\sqrt{2}\)
Xét ΔADC có \(cosDAC=\dfrac{AD^2+AC^2-CD^2}{2\cdot AD\cdot AC}\)
=>\(cos45=\dfrac{2a^2+4a^2-CD^2}{2\cdot a\sqrt{2}\cdot2a}\)
=>\(6a^2-CD^2=4a^2\cdot\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=4a^2\)
=>\(CD^2=2a^2\)
=>\(CD=a\sqrt{2}\)
Xét ΔCAD có \(CA^2+CD^2=AD^2\)
nên ΔCAD vuông tại C
=>CA\(\perp\)CD
CD\(\perp\)CA
CD\(\perp\)SA
SA,CA cùng thuộc mp(SAC)
Do đó: CD\(\perp\)(SAC)
b: CD\(\perp\)(SAC)
\(SC\subset\left(SAC\right)\)
Do đó: CD\(\perp\)SC
Đúng 1
Bình luận (0)