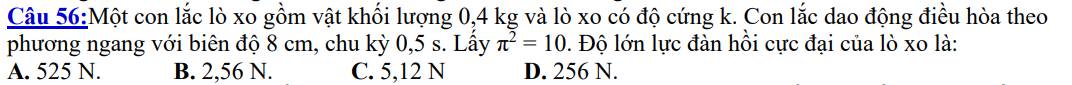Bài 2. Con lắc lò xo
Ta có: \(T=\dfrac{2\pi}{\omega}=2\pi\cdot\sqrt{\dfrac{k}{m}}\)\(\Rightarrow0,5=2\pi\cdot\sqrt{\dfrac{k}{0,4}}\)
\(\Rightarrow k=64N/m\)
\(F_{đhmax}=k\cdot A=64\cdot0,08=5,12N\)
Chọn C.
Đúng 2
Bình luận (0)
Một xe trượt có khối lượng 100g được gắn vào một lò xo có độ cứng k=400N/m . Xe trượt dao động trên một hệ thống đệm không khí đặt nằm ngang . Kéo xe đến vị trí lò xo dãn 20cm rồi thả nhẹ cho xe dao động . Xác định
a, biên độ , tần số góc , chu kì và tần số dao động của vật
b, Wđ , Wc , Wt của xe khi nó qua vị trí 20cm
c, thời điểm lần thứ 2024 lò xo nén 10cm
a)Biên độ: \(A=20cm=0,2m\)
Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{400}{0,1}}=20\sqrt{10}=20\pi\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{20\pi}=\dfrac{1}{10}=0,1s\)
Tần số dao động: \(f=\dfrac{1}{T}=\dfrac{1}{0,1}=10Hz\)
b)Tại vị trí \(A=20cm\):
\(W_đ=0J\)
\(W_{tmax}=W_c=\dfrac{1}{2}kx^2=\dfrac{1}{2}m\omega^2x^2=\dfrac{1}{2}\cdot0,1\cdot\left(20\pi\right)^2\cdot0,2^2=8J\)
c)Thời điểm lần thứ 2024 lò xo:
\(t_{2024}=2022+2=1011T+t'\)
\(t'=\dfrac{240}{360}T=\dfrac{2}{3}T=\dfrac{1}{15}s\)
\(t_{2024}=1011\cdot\dfrac{1}{10}+\dfrac{1}{15}=\dfrac{607}{6}s\approx101,17s\)
Đúng 3
Bình luận (1)
Câu 1: Một con lắc lò xo gồm vật nặng m0,4kg gắn vào đầu lò xo có độ cứng 40N/m. Người ta kéo quả nặng ra khỏi VTCB một đoạn 4cm rồi thả nhẹ cho nó dao động. Cơ năng dao động của con lắc là
A. 320J
B. 6,4.10-²J
C. 3,2J
D. 3,2.10-²J
Câu 2: Một con lắc lò xo dao động với pt x 2cos(20pi t +pi/2) cm. Biết khối lượng vật nặng m100g. Xđ chu kỳ và năng lượng của vật
A. 0,1s ; 78,9.10-³J
B. 0,1s ; 79,8.10-³J
C. 1s ; 7,89.10-³J
D. 1s ; 7,98.10-³J
Mn giúp mình với ạ. Mình cảm ơn nhiều!!!
Đọc tiếp
Câu 1: Một con lắc lò xo gồm vật nặng m=0,4kg gắn vào đầu lò xo có độ cứng 40N/m. Người ta kéo quả nặng ra khỏi VTCB một đoạn 4cm rồi thả nhẹ cho nó dao động. Cơ năng dao động của con lắc là A. 320J B. 6,4.10-²J C. 3,2J D. 3,2.10-²J Câu 2: Một con lắc lò xo dao động với pt x= 2cos(20pi t +pi/2) cm. Biết khối lượng vật nặng m=100g. Xđ chu kỳ và năng lượng của vật A. 0,1s ; 78,9.10-³J B. 0,1s ; 79,8.10-³J C. 1s ; 7,89.10-³J D. 1s ; 7,98.10-³J Mn giúp mình với ạ. Mình cảm ơn nhiều!!!
Câu 1:
\(W=\dfrac{1}{2}kA^2=\dfrac{1}{2}.40.0,04^2=0,032\left(J\right)=3,2.10^{-2}J\)
Chọn D
Câu 2:
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{20\pi}=0,1\left(s\right)\)
\(W=\dfrac{1}{2}kA^2=\dfrac{1}{2}\omega^2m.A^2\approx78,9.10^{-3}J\)
Chọn A
Đúng 1
Bình luận (0)
một con lắc lò xo có m=1kg k=1000n/m
lấy g=π2 =10m/skích thích cho vật giao động vs
pt x=10cos<ωt-2π/3>
a:tìm chu kì tần số và pha bân đầu
b:tìm vận tốc của vật khi qua vị tri có cân bằng và qua vị trí cí li độ x=6cm
c:tìm thế năng,động năng,cơ năng khi vật có li độ x=8cm
a, \(T=2\pi.\sqrt{\dfrac{m}{k}}\simeq0,2\left(s\right)\); f=1/T =5 dao dộng
-> \(w=\dfrac{2\pi}{T}=10\pi\left(\dfrac{Rad}{s}\right)\)
Pha ban đầu: \(\varphi=-\dfrac{2\pi}{3}\left(Rad\right)\)
b,\(A=\sqrt{x^2+\dfrac{v^2}{w^2}}\Leftrightarrow10=\sqrt{6^2+\dfrac{v^2}{\left(10\pi\right)^2}}\)
\(\Rightarrow v=\pm80\pi\left(\dfrac{cm}{s}\right)\)
c,tương tự b ta tính được \(v=\pm\dfrac{3}{5}\left(\dfrac{m}{s}\right)\)tại x=8
\(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}.1000.0,08^2=3,2J\)
\(W_d=\dfrac{1}{2}mv^2=1,8J\)
\(W=W_t+W_d=3,2+1,8=5J\)
Đúng 2
Bình luận (0)
Nhoừ mọi người giải giúp mình với ạ xin càm ơn ạ
1. Một lò xo có độ cứng k 25 N/m. Một đầu của lò xo gắn vào điểm O cố định. Treo vào lò xo một vật có khối lượng m 160 (g). Tần số góc của dao động là:A. omega12,5 (rad/s) B. omega12 (rad/s) C. omega10,5 (rad/s) D. omega13,5 (rad/s)2. Một con lắc lò xo dao động điều hòa, vật có khối lượng m0,2 kg. Trong 20left(sright) con lắc thực hiện được 50 dao động. Độ cứng của lò xo là:A. 60 N/m B. 40 N/m C. 50 N/m D. 55 N/m3. Con lắc lò...
Đọc tiếp
1. Một lò xo có độ cứng k = 25 N/m. Một đầu của lò xo gắn vào điểm O cố định. Treo vào lò xo một vật có khối lượng m = 160 (g). Tần số góc của dao động là:
A. \(\omega=12,5\) (rad/s) B. \(\omega=12\) (rad/s) C. \(\omega=10,5\) (rad/s) D. \(\omega=13,5\) (rad/s)
2. Một con lắc lò xo dao động điều hòa, vật có khối lượng \(m=0,2\) kg. Trong \(20\left(s\right)\) con lắc thực hiện được 50 dao động. Độ cứng của lò xo là:
A. 60 N/m B. 40 N/m C. 50 N/m D. 55 N/m
3. Con lắc lò xo gồm lò xo k và vật m, dao động điều hòa với tần số \(f=1\) Hz. Muốn f' = 0,5 Hz thì khối lượng của vật m' phải là:
A. m' = 2m B. m' = 3m C. m' = 4m D. m' = 5m
`1) \omega=\sqrt{k/[m}=\sqrt{25/[0,16]}=12,5(rad//s)`
`->\bb A`.
`2)T=t/N=20/50=0,4(s)`
`=>k=([2\pi]/T)^2 .m=([2\pi]/[0,4])^2 .0,2=50(N//m)`
`->\bb C`.
`3) m/[m']=[f' ^2]/[f^2]`
`=>[m]/[m']=1/4`
`=>m'=4m`
`->\bb C`.
Đúng 1
Bình luận (0)
Con lắc lò xo thẳng đứng vật có khối lượng 1kg , lò xo có độ cứng 100N/m , dao động điều hòa với biên độ 18cm , lấy g = 10 m/s^2 . Tính vận tốc của vật khi
a. Lò xo có chiều dài tự nhiên
b lò xo dãn 25 cm
Một vật dao động điều hoà có phương trình: x = 6cos(2\(\pi\)t - \(\pi\)/6)(cm). Tại thời điểm t, vật có li độ x= 3cm và vận tốc dương thì ở thời điểm 1/3s tiếp theo vật ở li độ
Để tính vị trí của vật điều hoà tại thời điểm 1/3 giây sau khi vật có li độ x = 3cm, chúng ta cần tính giá trị của x tại thời điểm đó.
Phương trình vật dao động điều hoà đã cho là: x = 6cos(2πt - π/6) (cm)
Để tìm thời điểm 1/3s tiếp theo, ta thay t = 1/3 vào phương trình trên:
x = 6cos(2π(1/3) - π/6) = 6cos(2π/3 - π/6) = 6cos(π/2) = 6 * 0 = 0 (cm)
Vậy, tại thời điểm 1/3s tiếp theo, vật sẽ ở li độ x = 0cm.
Đúng 0
Bình luận (0)
một vật dao động điều hòa với chu kì T. khoảng tgian trong một chu kì mà động năng nhỏ hơn ba lần thế năng là
Để tính khoảng thời gian trong một chu kỳ mà động năng nhỏ hơn ba lần thế năng của một vật dao động điều hoà, chúng ta có thể sử dụng công thức sau:
Tổng động năng = 3 * Tổng thế năng
Trong một chu kỳ, tổng động năng bằng tổng thế năng. Vì vậy, ta có:
3 * Tổng thế năng = Tổng thế năng
Từ đó, ta có:
2 * Tổng thế năng = 0
Vậy, khoảng thời gian trong một chu kỳ mà động năng nhỏ hơn ba lần thế năng là 0.
Đúng 0
Bình luận (0)