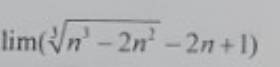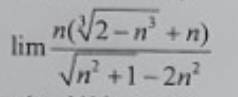Giúp em câu này vovới ạ
Bài 1: Giới hạn của dãy số
\(lim\left(\sqrt[3]{n^3-2n^2}-2n+1\right)\)
\(=lim\dfrac{n^3-2n^2-\left(2n-1\right)^3}{\left(\sqrt[3]{n^3-2n^2}\right)^2+\sqrt[3]{n^3-2n^2}\left(2n-1\right)+\left(2n-1\right)^2}\)
\(=lim\dfrac{n^3-2n^2-\left(8n^3-12n^2+6n-1\right)}{\sqrt[3]{n^6-4n^5+4n^4}+\sqrt[3]{n^3-2n^2}\left(2n-1\right)+4n^2-4n+1}\)
\(=lim\dfrac{-7n^3+10n^2-6n+1}{\sqrt[3]{n^6-4n^5+4n^4}+\sqrt[3]{n^3-2n^2}\left(2n-1\right)+4n^2-4n+1}\)
\(=lim\dfrac{-7+\dfrac{10}{n}-\dfrac{6}{n^2}+\dfrac{1}{n^3}}{\sqrt[3]{\dfrac{1}{n^3}-\dfrac{4}{n^4}+\dfrac{4}{n^5}}+\sqrt[3]{\dfrac{1}{n^3}-\dfrac{2}{n^4}}\left(2-\dfrac{1}{n}\right)+\dfrac{4}{n}-\dfrac{4}{n^2}+\dfrac{1}{n^3}}\)
\(=\dfrac{-7}{0}=-\infty\)
Đúng 2
Bình luận (2)
\(\lim\limits\dfrac{n\left(\sqrt[3]{2-n^3}+n\right)}{\sqrt{n^2+1}-2n^2}\)
\(=lim\dfrac{n\cdot n\cdot\left(\sqrt[3]{\dfrac{2}{n^3}-1}+1\right)}{n^2\left(\sqrt{\dfrac{1}{n^2}+\dfrac{1}{n^4}}-2\right)}\)
\(=\lim\limits\dfrac{\sqrt[3]{\dfrac{2}{n^3}-1}+1}{\sqrt{\dfrac{1}{n^2}+\dfrac{1}{n^4}}-2}=\dfrac{\sqrt[3]{0-1}+1}{0-2}=\dfrac{-1+1}{-2}=0\)
Đúng 1
Bình luận (0)
tìm dạng khai triển của cấp số nhân lùi vô hạn Un, biết tổng bằng 32, U2= 8
\(\dfrac{u_2}{q\left(1-q\right)}=32\rightarrow\dfrac{8}{q\left(1-q\right)}=32\rightarrow q=\dfrac{1}{2}\rightarrow u_1=16\\ \rightarrow u_n=16\left(\dfrac{1}{2}\right)^{n-1}=2^{5-n}\)
Đúng 0
Bình luận (0)
tìm dạng khai triển của cấp số nhân lùi vô hạn biết tổng = 32, U2 = 8
Tìm \(\lim\left(\sqrt{n^2+7}-\sqrt{n^2+5}\right)\).
\(\lim\limits\left(\sqrt{n^2+7}-\sqrt{n^2+5}\right)\)
\(=\lim\limits\dfrac{n^2+7-n^2-5}{\sqrt{n^2+7}+\sqrt{n^2+5}}\)
\(=\lim\limits\dfrac{2}{\sqrt{n^2+7}+\sqrt{n^2+5}}\)
\(=\lim\limits\dfrac{\dfrac{2}{n}}{\sqrt{1+\dfrac{7}{n^2}}+\sqrt{1+\dfrac{5}{n^2}}}=\dfrac{0}{\sqrt{1}+\sqrt{1}}=0\)
Đúng 1
Bình luận (0)
Tìm \(\lim\left(n+\sqrt{n^2-n+1}\right)\).
\(\lim\limits\left(n+\sqrt{n^2-n+1}\right)\)
\(=\lim\limits\dfrac{n^2-\left(n^2-n+1\right)}{n-\sqrt{n^2-n+1}}\)
\(=\lim\limits\dfrac{n^2-n^2+n-1}{n-\sqrt{n^2\left(1-\dfrac{1}{n}+\dfrac{1}{n^2}\right)}}\)
\(=\lim\limits\dfrac{n-1}{n-n\cdot\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}}\)
\(=\lim\limits\dfrac{1-\dfrac{1}{n}}{1-\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}}=+\infty\)
Vì \(\left\{{}\begin{matrix}\lim\limits1-\dfrac{1}{n}=1-0=1\\\lim\limits\left(1-\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}\right)=1-\sqrt{1-0+0}=1-1=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm \(\lim\left(\sqrt[3]{1+2n-n^3}-n\right)\).
\(\lim\limits\left(\sqrt[3]{1+2n-n^3}-n\right)\)
\(=\lim\limits\dfrac{1+2n-n^3-n^3}{\sqrt[3]{\left(1+2n-n^3\right)^2}+n\cdot\sqrt[3]{1+2n-n^3}+n^2}\)
\(=\lim\limits\dfrac{1+2n-2n^3}{\sqrt[3]{\left(1+2n-n^3\right)^2}+n\cdot\sqrt[3]{1+2n-n^3}+n^2}\)
\(=\lim\limits\dfrac{n^3\left(-2+\dfrac{2}{n^2}+\dfrac{1}{n^3}\right)}{n^2\cdot\sqrt[3]{\left(\dfrac{1}{n^3}+\dfrac{2}{n^2}-1\right)^2}+n^2\cdot\sqrt[3]{-1+\dfrac{2}{n^2}+\dfrac{1}{n^3}}+n^2}\)
\(=\lim\limits\dfrac{n\left(-2+\dfrac{2}{n^2}+\dfrac{1}{n^3}\right)}{\sqrt[3]{\left(\dfrac{1}{n^3}+\dfrac{2}{n^2}-1\right)^2}+\sqrt[3]{-1+\dfrac{2}{n^2}+\dfrac{1}{n^3}}+1}\)
\(=-\infty\) vì \(\left\{{}\begin{matrix}\lim\limits n=+\infty\\\lim\limits\dfrac{-2+\dfrac{2}{n^2}+\dfrac{1}{n^3}}{\sqrt[3]{\left(\dfrac{1}{n^3}+\dfrac{2}{n^2}-1\right)^2}+\sqrt[3]{-1+\dfrac{2}{n^2}+\dfrac{1}{n^3}}+1}=\dfrac{-2}{1+1+1}=-\dfrac{2}{3}< 0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Phương pháp: Nhân cả tử và mẫu với biểu thức liên hợp
1. \(A\pm B\) có liên hợp là \(A\mp B\).
2. \(\sqrt{A}\pm B\) có liên hợp là \(\sqrt{A}\mp B\).
3. \(\sqrt{A}\pm\sqrt{B}\) có liên hợp là \(\sqrt{A}\mp\sqrt{B}\).
4. \(\sqrt[3]{A}\pm B\) có liên hợp là \(\sqrt[3]{A^2}\mp B\sqrt[3]{A}+B^2\).
Bài giải: Áp dụng biểu thức liên hợp số 4
\(\lim\left(\sqrt[3]{1+2n-n^3}-n\right)\)
\(=\lim\dfrac{\left(\sqrt[3]{1+2n-n^3}-n\right)\left[\sqrt[3]{\left(1+2n-n^3\right)^2}+n\sqrt[3]{1+2n-n^3}+n^2\right]}{\sqrt[3]{\left(1+2n-n^3\right)^2}+n\sqrt[3]{1+2n-n^3}+n^2}\)
\(=\lim\dfrac{1+2n-n^3-n^3}{\sqrt[3]{n^6-4n^4-2n^3+4n^2+4n+1}+\sqrt[3]{n^3+2n^4-n^6}+n^2}\)
\(=\lim\dfrac{\left(1+2n-2n^3\right)\div n^3}{\left(\sqrt[3]{n^6-4n^4-2n^3+4n^2+4n+1}+\sqrt[3]{n^3+2n^4-n^6}+n^2\right)\div n^3}\)
\(=\lim\dfrac{\dfrac{1}{n^3}+\dfrac{2}{n^2}-2}{\sqrt[3]{\dfrac{1}{n^3}-\dfrac{4}{n^5}-\dfrac{2}{n^6}+\dfrac{4}{n^7}+\dfrac{4}{n^8}+\dfrac{1}{n^9}}+\sqrt[3]{\dfrac{1}{n^6}+\dfrac{2}{n^5}-\dfrac{1}{n^3}}+\dfrac{1}{n}}\)
\(=-\infty\)
(vì \(\lim\left(\dfrac{1}{n^3}+\dfrac{2}{n^2}-2\right)=-2\) và \(\lim\left(\sqrt[3]{\dfrac{1}{n^3}-\dfrac{4}{n^5}-\dfrac{2}{n^6}+\dfrac{4}{n^7}+\dfrac{4}{n^8}+\dfrac{1}{n^9}}+\sqrt[3]{\dfrac{1}{n^6}+\dfrac{2}{n^5}-\dfrac{1}{n^3}}+\dfrac{1}{n}\right)=0\), chia được \(\dfrac{-2}{0}\) nên ra \(-\infty\))
Đúng 0
Bình luận (0)
Tính \(\lim\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{16}+...+\dfrac{1}{n^2}\right)\).
Sử dụng những kiến thức tính đến bài "Bài 1: Giới hạn của dãy số". Giải thích chi tiết bước làm.
Tính \(\lim\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{16}+...+\dfrac{1}{n^2}\right)\).
Chỉ giải bằng những kiến thức có trong bài "Bài 1: Giới hạn của dãy số". Giải thích chi tiết bước làm và tại sao lại làm như vậy.