Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
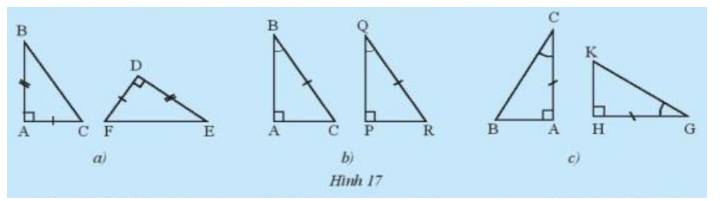
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.

Tìm các tam giác vuông bằng nhau trong mỗi hình bên (Hình 19).
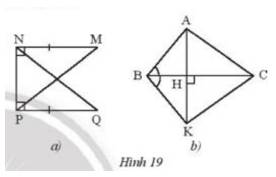
Thảo luận (1)Hướng dẫn giảia) Xét \(\Delta{MNP} và \Delta{QPN}\), ta có:
NM = PQ
NP chung
\(\widehat {MNP} = \widehat {NPQ}\)
\(\Rightarrow \Delta{MNP} =\Delta{QPN}\) (c.g.c)
b) Ta thấy\(\Delta{ABH}=\Delta{KBH}\) (g-c-g) và \(\Delta{AHC}=\Delta{KHC}\)(c-g-c)
\(\Delta{ABC}=\Delta{KBC}\)
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC vuông tại A trong Hình 20a. Vẽ lên tờ giấy tam giác vuông A’B’C’có cạnh huyền và một cạnh góc vuông bằng với cạnh huyền và một cạnh góc vuông của tam giác ABC như sau:
- Vẽ góc vuông xA’ý, trên cạnh A’y vẽ đoạn A’C’= AC.
- Vẽ cung tròn tâm C’ bán kính bằng BC cắt A’x tại B’
Cắt rời tam giác A’B’C’. Em hãy cho biết có thể đặt chồng khít tam giác này lên tam giác kia không.
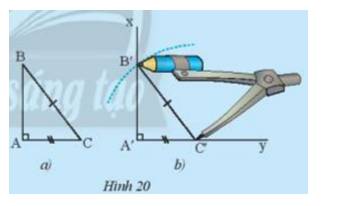
Thảo luận (1)Hướng dẫn giảiTa nhận thấy 2 hình bằng nhau (chồng lên nhau vì vừa khít)
(Trả lời bởi Hà Quang Minh)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
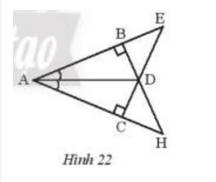
Thảo luận (1)Hướng dẫn giải+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)
(Trả lời bởi Hà Quang Minh)
Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.
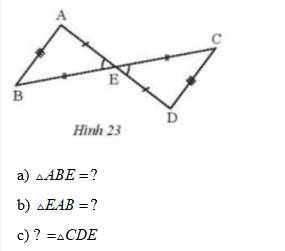
Thảo luận (2)Hướng dẫn giải\(a,\Delta ABE=\Delta DCE\\ b,\Delta EAB=\Delta ECD\\ c,\Delta BAE=\Delta CDE\)
(Trả lời bởi Hà Quang Minh)
Cho \(\Delta{DEF}=\Delta{HIK}\) và \(\widehat D= {73^o}\), DE = 5cm, IK = 7cm. Tính số đo \(\widehat H\) và độ dài HI, EF.
Thảo luận (1)Hướng dẫn giảiVì \(\Delta{DEF}=\Delta{HIK}\)
\( \Rightarrow \widehat D = \widehat H\)( 2 góc tương ứng )
Mà \(\widehat D =73^0\)
\( \Rightarrow \widehat H=73^0\)
Vì \(\Delta{DEF}=\Delta{HIK}\)
\(\Rightarrow DE = HI;EF = IK;DF = HK\)( các cạnh tương ứng )
Vậy \( \widehat H = {73^o}; HI = 5cm; EF = 7cm\)
(Trả lời bởi Hà Quang Minh)
Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó \(\widehat A = \widehat E\), \(\widehat C = \widehat D\). Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.
Thảo luận (1)Hướng dẫn giảiVì \(\widehat A = \widehat E\), \(\widehat C = \widehat D\) nên đỉnh A tương ứng với đỉnh E, đỉnh C tương ứng với đỉnh D.
\( \Rightarrow \widehat B = \widehat F\) ( 2 góc tương ứng)
Do đó, \(\Delta{ABC}=\Delta{EFD}\)
\(\Rightarrow AB = DE;BC = EF;AC = DF\)( các cạnh tương ứng )
(Trả lời bởi Hà Quang Minh)
Cho biết \(\Delta{MNP}=\Delta{DEF}\) và MN = 4cm, MP = 5cm, EF = 6cm. Tính chu vi tam giác MNP.
Thảo luận (1)Hướng dẫn giảiVì \(\Delta{MNP}=\Delta{DEF}\)
\( \Rightarrow DE = MN;EF = NP;DF = MP\) (các cạnh tương ứng)
\( \Rightarrow NP = 6cm\)
\( \Rightarrow \) Chu vi tam giác MNP là:
C = MN + MP + NP = 4 + 5 + 6 = 15 (cm)
(Trả lời bởi Hà Quang Minh)
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.
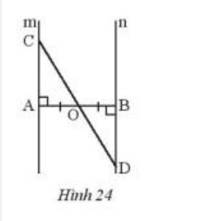
Thảo luận (1)Hướng dẫn giảiXét \(\Delta OAC\) và \(\Delta OBD\), ta có:
\(\widehat {COA} = \widehat {BOD}\) ( 2 góc đối đỉnh)
AO = BO
\(\widehat A = \widehat B\)
\(\Rightarrow \Delta OAC=\Delta OBD\) ( g-c-g )
\( \Rightarrow CO = DO\) ( cạnh tương ứng )
\( \Rightarrow \) O là trung điểm CD
(Trả lời bởi Hà Quang Minh)
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) \(\Delta EFH=\Delta HGE\)
b) EF // HG
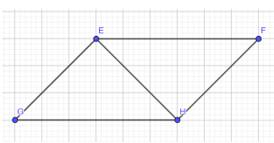
Thảo luận (1)Hướng dẫn giảia) Xét \(\Delta EFH\) và \(\Delta HGE\) có :
EF = HG; FH = GE; EH chung
\(\Rightarrow \Delta EFH=\Delta HGE\) (c-c-c)
\( \Rightarrow \widehat {FEH} = \widehat {EHG}\)( 2 góc tương ứng )
b) Vì \(\widehat {FEH}=\widehat {EHG}\)
Mà 2 góc này ở vị trí so le trong
Do đó, EF // HG (Dấu hiệu nhận biết)
(Trả lời bởi Hà Quang Minh)